Đề bài
Cho hình thang vuông ABCD có ˆA=ˆD=900 , AB=2a,CD=a,AD=3a M là điểm bất kì thuộc đoạn thẳng AD.
a) Xác định vị trí điểm M để hai đường thẳng BM và CM vuông góc với nhau.
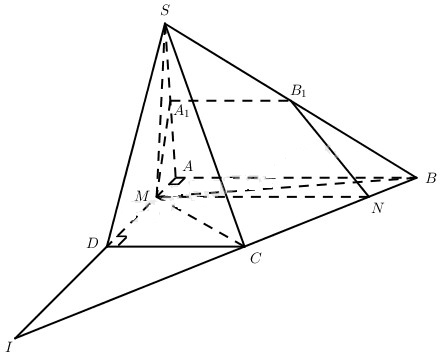
b) Gọi S là điểm thuộc đường thẳng vuông góc với mp(ABC) kẻ từ điểm M sao cho SM = AM. Xét mặt phẳng (P) đi qua M và vuông góc với SA. Thiết diện của hình chóp S.ABCD cắt bởi (P) là hình gì? Tính diện tích thiết diện thu được theo a và x, ở đây x=AM(0<x≤3a).
Lời giải chi tiết
a) Đặt AM=x thì DM=3a−x.
Dễ thấy BC=a√10
MB2=4a2+x2MC2=a2+(3a−x)2
Hai đường thẳng BM và CM vuông góc với nhau khi và chỉ khi
BC2=MB2+MC2⇔10a2=2x2+14a2−6ax⇔x2−3ax+2a2=0⇒x=a,x=2a
Vậy có hai vị trí của M để MB và MC vuông góc với nhau.
b) Vì SM⊥(ABCD),AB⊥MA nên AB⊥SA (định lí ba đường vuông góc). Mặt khác (P)⊥SA nên (P) // AB.
Do MA = MS, (P) đi qua M và (P)⊥SA nên (P) cắt SA tại trung điểm A1 của SA. Từ đó (P) cắt (SAB) theo giao tuyến A1B1 với A1B1 // AB; (P) cắt (ABCD) theo giao tuyến MN song song với AB. Như vậy, thiết diện của hình chóp S.ABCD khi cắt bởi mp(P) là hình thang vuông M A1B1N (tứ giác M A1B1N là hình thang vuông MN // A1B1, ngoài ta AB⊥(SAD) nên A1B1⊥(SAD), tức là A1B1⊥MA1)
SMA1B1N=12(A1B1+MN).A1MA1B1=12AB=a,A1M=12SA=x√22
Gọi I là giao điểm của AD và BC thì IA = 6a. Ta có
MNAB=IMIA⇔MN2a=6a−x6a⇒MN=6a−x3
Vậy
SMA1B1N=12(a+6a−x3).x√22=√2(9a−x)x12(voi0<x≤3a).
