Đề bài
Cho hình chóp S.ABCD. Trên cạnh SC lấy một điểm E không trùng với hai điểm S và C.
a) Tìm giao điểm F của đường thẳng SD với mp(ABE).
b) Giả sử AB không song song với CD, hãy chứng minh ba đường thẳng AB, CD và EF đồng quy.
Lời giải chi tiết
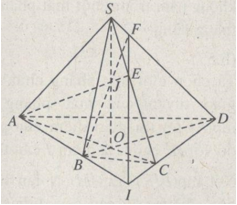
a) Gọi O là giao điểm của AC và BD; J là giao điểm của SO và AE. Hai mặt phẳng (SBD) và (ABE) có hai điểm chung là B và J. Do đó \(\left( {SBD} \right) \cap \left( {ABE} \right) = BJ\).
Gọi F là giao điểm của BJ và SD thì F chính là giao điểm của đường thẳng SD với mp(ABE).
b) Gọi I là giao điểm của AB và CD. Khi đó ba điểm I, E F cùng thuộc hai mặt phẳng (ABE) và (SCD) nên chúng thẳng hàng.

