Đề bài
Cho tứ diện SABC, hai mặt phẳng (SAB) và (SBC) vuông góc với nhau và có SA vuông góc với mp(ABC), SB=a√2,^BSC=450,^ASB=α.
a) Chứng minh rằng BC vuông góc với SB. Tìm điểm cách đều các điểm S, A, B, C.
b) Xác định α để hai mặt phẳng (SCA) và (SCB) tạo với nhau góc 60°.
Lời giải chi tiết
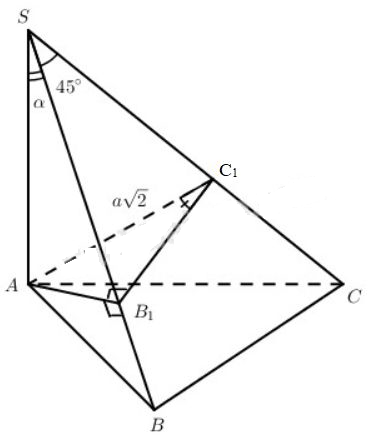
a) Vì
(ABC)⊥(SAB)(SBC)⊥(SAB)
mà BC=(ABC)∩(SBC) nên BC⊥(SAB)⇒BC⊥SB.
Như vậy, tứ diện SABC có ^SAC=900 và ^SBC=900 nên điểm cách đều S, A, B, C là trung điểm của SC.
Chú ý. Có thể chứng minh BC⊥SB như sau:
Kẻ AB1⊥SB do (SAB)⊥(SBC) nên AB1⊥(SBC)
⇒AB1⊥BC
mặt khác BC⊥SA
⇒BC⊥(SAB)⇒BC⊥SB
b) Kẻ AB1⊥SB,AC1⊥SC, dễ chứng minh được
AB1⊥(SBC) và (AB1C1)⊥SC.
Từ đó ^AC1B1 là góc giữa hai mặt phẳng (SCA) và (SCB).
Xét ∆AB1C1 ta có AB1=B1C1tan600
mà AB1=SB1tanα,B1C1=SB1sin450.
Vậy hai mặt phẳng (SCA) và (SCB) tạo với nhau góc 60° khi và chỉ khi
SB1tanα=SB1.√22.√3⇔tanα=√62.
Hệ thức này xác định α.

