Đề bài
Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng a, \(\widehat {BA{\rm{D}}} = {60^0},\widehat {BAA'} = \widehat {DAA'} = {120^0}\) .
a) Tính góc giữa các cặp đường thẳng AB với A’D và AC’ với B’D.
b) Tính diện tích các hình A’B’CD và ACC’A’.
c) Tính góc giữa đường thẳng AC’ và các đường thẳng AB, AD, AA’.
Lời giải chi tiết
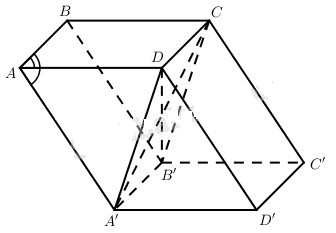
Đặt \(\overrightarrow {AB} = \overrightarrow x ,\overrightarrow {A{\rm{D}}} = \overrightarrow y ,\overrightarrow {AA'} = \overrightarrow z \) thì
\(\eqalign{ & {\overrightarrow x ^2} = {\overrightarrow y ^2} = {\overrightarrow z ^2} = {a^2} \cr & \overrightarrow x .\overrightarrow y = {{{a^2}} \over 2}; \cr & \overrightarrow x .\overrightarrow z = - {{{a^2}} \over 2}; \cr & \overrightarrow y .\overrightarrow z = - {{{a^2}} \over 2} \cr} \)
a) Vì AB // A’B’ nên góc giữa AB và A’D bằng góc giữa A’B’ và A’D, đó là góc \(\widehat {DA'B'}\) hoặc \({180^0} - \widehat {DA'B'}\) .
Đặt \(\widehat {DA'B'} = \alpha \).
Ta có:
\(\eqalign{ & A'D = a\sqrt 3 ,A'B' = a \cr & \overrightarrow {DB'} = \overrightarrow x - \overrightarrow y + \overrightarrow z \cr & \Rightarrow {\overrightarrow {DB'} ^2} = 3{{\rm{a}}^2} - {a^2} - {a^2} + {a^2} = 2{{\rm{a}}^2} \cr} \)
Vậy \(2{{\rm{a}}^2} = {a^2} + 3{{\rm{a}}^2} - 2{\rm{a}}.a\sqrt 3 \cos \alpha \Rightarrow \cos \alpha = {1 \over {\sqrt 3 }}\).
Như thế góc giữa A’D và AB bằng α mà \(\cos \alpha = {1 \over {\sqrt 3 }}\)
\(\eqalign{ & \overrightarrow {AC'} = \overrightarrow x + \overrightarrow y + \overrightarrow z \cr & \Rightarrow {\overrightarrow {AC'} ^2} = 3{a^2} + {a^2} - {a^2} - {a^2} = 2{a^2} \cr} \)
Dễ thấy AB’ = a.
Ta có ADC’B’ là hình bình hành mà AD = AB’, AC’ = B’D nên tứ giác ADC’B’ là hình vuông. Vậy AC’ ⊥ B’D, tức là góc giữa AC’ và B’D bằng 90°.
b)
\({S_{A'B'C{\rm{D}}}} = A'D.A'B'\sin \widehat {DA'B'} = a\sqrt 3 .a.{{\sqrt 6 } \over 3}\) .
Vậy \({S_{A'B'C{\rm{D}}}} = {a^2}\sqrt 2 \)
Đặt \(\widehat {ACC'} = \beta \) thì \(AC{'^2} = A{C^2} + CC{'^2} - 2{\rm{A}}C.CC'.\cos \beta \)
hay
\(\eqalign{ & 2{a^2} = 3{a^2} + {a^2} - 2a\sqrt 3 .a.\cos \beta \cr & \Rightarrow \cos \beta = {1 \over {\sqrt 3 }} \Rightarrow \sin \beta = {{\sqrt 6 } \over 3} \cr} \)
Vậy \({S_{ACC'A'}} = AC.CC'.\sin \beta = a\sqrt 3 .a.{{\sqrt 6 } \over 3} = {a^2}\sqrt 2 \)
c) Do \(\overrightarrow {AC'} = \overrightarrow x + \overrightarrow y + \overrightarrow z \)
Suy ra:
\(\eqalign{ & \overrightarrow {AC'} .\overrightarrow {AB} = \left( {\overrightarrow x + \overrightarrow y + \overrightarrow z } \right)\overrightarrow x \cr & = {a^2} + {{{a^2}} \over 2} - {{{a^2}} \over 2} = {a^2} \cr} \)
hay
\(\eqalign{ & \left| {\overrightarrow {AC'} } \right|\left| {\overrightarrow {AB} } \right|\cos \gamma = {a^2} \cr & \Rightarrow \cos \gamma = {1 \over {\sqrt 2 }} \Rightarrow \gamma = {45^0} \cr} \)
Vậy góc giữa AC’ và AB bằng 45°.
\(\eqalign{ & \overrightarrow {AC'} .\overrightarrow {A{\rm{D}}} = \left( {\overrightarrow x + \overrightarrow y + \overrightarrow z } \right)\overrightarrow y \cr & = {{{a^2}} \over 2} + {a^2} - {{{a^2}} \over 2} = {a^2} \cr} \)
hay
\(\eqalign{ & \left| {\overrightarrow {AC'} } \right|.\left| {\overrightarrow {A{\rm{D}}} } \right|\cos \varphi = {a^2} \cr & \Rightarrow \cos \varphi = {1 \over {\sqrt 2 }} \Rightarrow \varphi = {45^0} \cr} \)
Vậy góc giữa AC’ và AD bằng 45°.
\(\eqalign{ & \overrightarrow {AC'} .\overrightarrow {AA'} = \left( {\overrightarrow x + \overrightarrow y + \overrightarrow z } \right)\overrightarrow z \cr & = - {{{a^2}} \over 2} - {{{a^2}} \over 2} + {a^2} = 0 \cr} \)
Vậy góc giữa AC’ và AA’ bằng 90°.

