Gọi (P) và (P’) lần lượt là đồ thị của hai hàm số
LG a
Vẽ các đồ thị của hai hàm số đó trên cùng một hệ trục tọa độ.
Lời giải chi tiết:
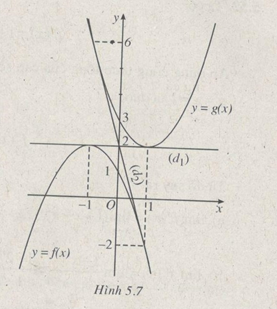
LG b
Viết phương trình của đường thẳng (d) là tiếp tuyến của (P) để tiếp điểm A đồng thời cũng là tiếp tuyến của (P’) tại tiếp điểm B (đường thẳng (d) nếu có, được gọi là tiếp tuyến chung của (P) và (P’).
Lời giải chi tiết:
Gọi đường thẳng y=mx+p(d) là tiếp tuyến của đồ thị hàm số y=f(x)=−x2−2x+1 tại điểm A(a;f(a)), đồng thời là tiếp tuyến của đồ thị hàm số y=g(x)=x2−2x+3 tại điểm B(b;g(b)). Nếu thế thì ta phải có
(I){f′(a)=g′(b)=m(1)f(a)=ma+p(2)g(b)=mb+p(3)
((I) chứng tỏ hệ số góc của tiếp tuyến tại A (đối với (P) và hệ số góc của tiếp tuyến B (đối với (P’)) bằng nhau và bằng m; (2) chứng tỏ đường thẳng (d) đi qua đoạn A; (3) chứng tỏ đường thẳng (d) đi qua B)
Khử m và p ở hệ phương trình (1), ta được
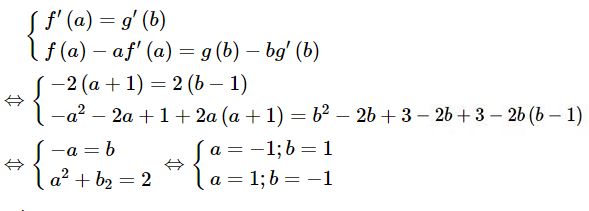
Thế vào (1) ta được
- Với a=−1;b=1 thì m=0 và p=2, suy ra tiếp tuyến chung phải tìm là y=2(d1)
- Với a=1;b=−1 thì m=−4 và p=2, suy ra tiếp tuyến chung phải tìm là y=−4x+2(d2)

