Đề bài
Cho hai đường tròn có bán kính bằng nhau (O) và (O’). Trên (O) lấy hai bán kính vuông góc OA, OB và trên (O’) lấy hai bán kính vuông góc O’A’, O’B’ sao cho A, A’ nằm trên đường thẳng OO’ và hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {O'A'} \) cùng hướng, còn hai vectơ \(\overrightarrow {OB} \) và \(\overrightarrow {O'B'} \) ngược hướng.
a) Chứng minh rằng có phép dời hình F biến đường tròn (O) thành (O’) sao cho hai điểm A, B lần lượt biến thành hai điểm A’, B’.
b) Với mỗi điểm M nằm trên (O) và ảnh M’ của nó qua phép dời hình F, chứng minh rằng trung điểm của đoạn thẳng MM’ nằm trên một đường thẳng cố định.
Lời giải chi tiết
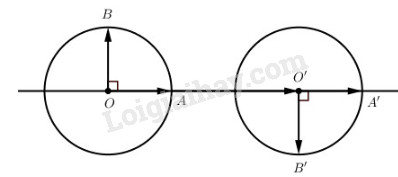
a) Vì hai tam giác OAB và O’A’B’ bằng nhau nên có phép dời hình F biến O thành O’, biến A thành A’ và biến B thành B’. Hiển nhiên F cũng biến (O) thành (O’).
b) Gọi f là phép đối xứng trượt có trục OO’ và vectơ trượt là \(\overrightarrow v = \overrightarrow {OO'} \) thì rõ ràng f biến O, A, B lần lượt thành O’, A’, B’. Vậy f trùng F.
Từ đó, suy ra trung điểm của MM’ luôn luôn nằm trên đường thẳng OO’.

