Đề bài
Cho hình tứ diện ABCD có tất cả các cạnh bằng m. Các điểm M và N lần lượt là trung điểm của AB và CD.
a) Tính độ dài MN.
b) Tính góc giữa đường thẳng MN với các đường thẳng BC, AB và CD.
Lời giải chi tiết
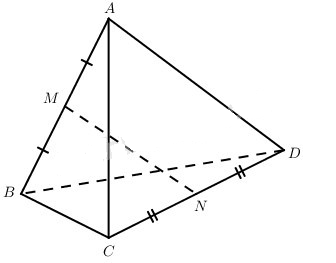
Đặt →AD=→a,→AB=→b,→AC=→c .
Khi đó, ta có:
→a.→b=→b.→c=→c.→a=12m2 và →a2=→b2=→c2=m2
a) Vì M, N là trung điểm của AB và CD nên
→MN=12(→AD+→BC)
hay →MN=12(→a+→c−b)
Vậy
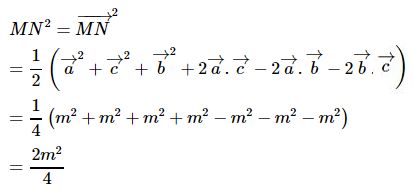
Tức là MN=m√22
b) Ta có
→MN.→AB=12(→a+→c−→b).→b=12(→a.→b+→b.→c−→b2)=12(m22+m22−m2)=0
Vậy góc giữa hai đường thẳng MN và AB bằng 90°
Ta có:
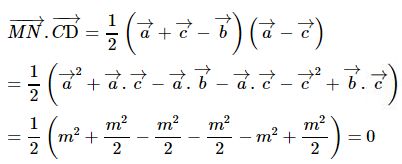
Vậy góc giữa hai đường thẳng MN và CD bằng 90°.
Ta có :
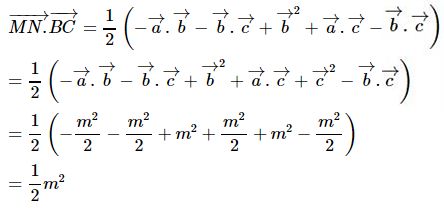
Tức là:
|→MN|.|→BC|cos(→MN,→BC)=12m2
Từ đó cos(→MN,→BC)=m22m.m√22=√22
Vậy góc giữa hai đường thẳng MN và BC bằng 45°.

