Đề bài
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M và N lần lượt là trọng tâm của tam giác SAB và SAD; E là trung điểm của CB.
a) Chứng minh rằng MN//BD.
b) Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mp(MNE).
c) Gọi H và L lần lượt là các giao điểm của mp(MNE) với cạnh SB và SD. Chứng minh rằng LH//BD.
Lời giải chi tiết
a) Gọi M’ và N’ lần lượt là trung điểm của AB và AD. Dễ thấy:
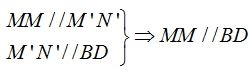
b) Ta có:
\(\eqalign{
& MM \subset \left( {MNE} \right) \cr
& BD \subset \left( {ABCD} \right) \cr
& MN//BD \cr
& \Rightarrow \left( {MNE} \right) \cap \left( {ABCD} \right) = Ex \cr} \)
thỏa mãn Ex // MN // BD.
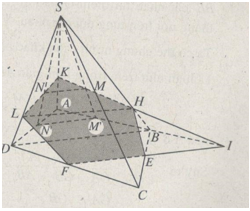
Vậy từ E kẻ đường thẳng song song với BD lần lượt cắt CD, AB tại F, I. Nối IM lần lượt cắt SB và SA tại H và K; nối KN cắt SD tại L. Thiết diện cần tìm là ngũ giác KLFEH.
c) Ta có:
\(\eqalign{
& NM \subset mp\left( {MNE} \right) \cr
& DB \subset mp\left( {SBD} \right) \cr
& MN//DB \cr} \)
Và \(\left( {MNE} \right) \cap \left( {SBD} \right) = LH\)
Suy ra: LH // DB.

