Đề bài
Ta gọi phần nguyên của số thực x là số nguyên lớn nhất không lớn hơn x và kí hiệu nó là \(\left[ x \right].\)
Chẳng hạn \(\left[ 5 \right] = 5;\left[ {3,12} \right] = 3;\left[ { - 2,725} \right] = - 3.\) vẽ đồ thị ghàm số \(y = \left[ x \right]\) và tìm
\(\mathop {\lim }\limits_{x \to {3^ + }} \left[ x \right],\mathop {\lim }\limits_{x \to {3^ - }} \left[ x \right]\) và \(\mathop {\lim }\limits_{x \to 3} \left[ x \right]\) (nếu có).
Lời giải chi tiết
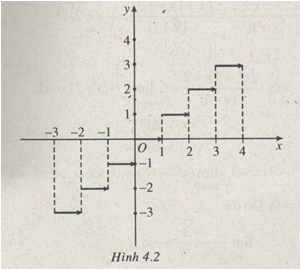
Đồ thị (h.4.2).Với \(2 < x<3;\left[ x \right] = 2\) ; do đó \(\mathop {\lim }\limits_{x \to {3^ - }} \left[ x \right] = 2.\)
Với \(3 < x < 4,\left[ x \right] = 3\) ; do đó \(\mathop {\lim }\limits_{x \to 3 ^+ } \left[ x \right] = 3.\)
Vì \(\mathop {\lim }\limits_{x \to {3^ - }} \left[ x \right] \ne \mathop {\lim }\limits_{x \to {3^ + }} \left[ x \right]\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 3} \left[ x \right]\).