Đề bài
Cho năm điểm M, N, P, Q, R. Hãy xác định ngũ giác ABCDE sao cho M, N, P, Q, R lần lượt là trung điểm các cạnh AB, BC, CD, DE, EA của ngũ giác đó.
Lời giải chi tiết
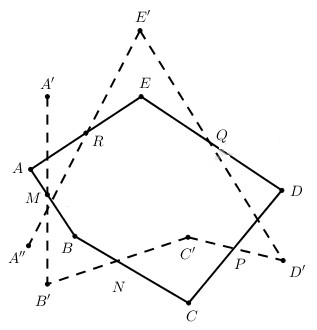
Giả sử đã xác định được ngũ giác ABCDE thỏa mãn yêu cầu của bài toán. Lấy một điểm A bất kì và xác định các điểm B’, C’, D’, E’, A’’ như sau: B’ là điểm đối xứng của A’ qua M, C’ là điểm đối xứng của B qua N, D’ là điểm đối xứng của C’ qua P, E’ là điểm đối xứng của D’ qua Q, và A’’ là điểm đối xứng của E’ qua R.
Theo các tính chất của phép đối xứng tâm ta có:
\(\eqalign{ & \overrightarrow {AA'} = - \overrightarrow {BB'} = \overrightarrow {CC'} \cr & =- \overrightarrow {DD'} = \overrightarrow {EE'} = - \overrightarrow {AA''} \cr} \)
Suy ra \(\overrightarrow {AA'} = \overrightarrow { - AA''} \), do đó A là trung điểm của đoạn thẳng A’A’’.
Từ đó suy ra cách dựng: Lấy điểm A’ tùy ý rồi dựng các điểm B’, C’, D’, E’, A’’ như trên. Dựng A là trung điểm của đoạn thẳng A’A’’. Có điểm A ta dễ dàng dựng được các điểm B, C, D và E.
