Đề bài
Trong mặt phẳng tọa độ, đồ thị (C) của hàm số \(y = 2x + 1.\) Trên (C) lấy điểm \({A_1}\) có hoành độ bằng \({1 \over 3}.\) Qua \({A_1}\) kẻ một đường thẳng song song với trục hoành cắt đường thẳng \(\Delta \) chứa đường phân giác của góc phần tư thứ nhất tại điểm \({B_1};\) gọi \({A_2}\) là giao điểm của (C) với đường thẳng đi qua \({B_1}\) và song song với trục tung. Với điểm \({A_2},\) lại thực hiện các bước tương tự như đã làm với điểm \({A_1}\) ta sẽ được điểm \({A_3}.\) Với điểm \({A_3},\) lại làm như thế với điểm \({A_4}.\) Cứ tiếp tục mãi quá trình trên, ta sẽ được một dãy vô hạn các điểm \({A_1},{A_2},{A_3},{A_4},...\) nằm trên đồ thị (C), (h.3.1)
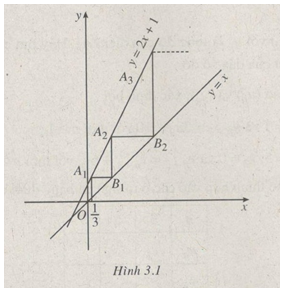
Với mỗi số nguyên dương n, gọi \({u_n}\) là hoành độ của điểm \({A_n}.\) Hãy cho dãy số \(\left( {{u_n}} \right)\) bởi hệ thức truy hồi.
Lời giải chi tiết
- Phương trình của đường thẳng \(\Delta :y = x\)
- Với mỗi \(n \ge 1,\) kí hiệu \({a_n}\) và \({b_n}\) tương ứng là tung độ của điểm \({A_n}\) và điểm \({B_{n.}}\) Khi đó:
- Do \({A_n}\) nằm trên (C) nên \({a_n} = 2{u_n} + 1\)
- Do \({B_n}\) nằm trên đường thẳng đi qua \({A_n}\) và song song với trục hoành nên \({b_n} = {a_n} = 2{u_n} + 1\)
- Do \({B_n}\) nằm trên đường thẳng đi qua \({A_{n + 1}}\) và song song với trục tung nên hoành độ của nó bằng \({u_{n + 1}}\)
Từ đó, do \({B_n}\) nằm trên \(\Delta \) nên \({u_{n + 1}} = {b_n} = 2{u_n} + 1\) với mọi \(n \ge 1\)
Vậy, dãy số \(\left( {{u_n}} \right)\) được xác định bởi \({u_1} = {1 \over 3}\) và \({u_{n + 1}} = 2{u_n} + 1\) với mọi \(n \ge 1\)

