Đề bài
Trong mặt phẳng (P), cho hình thoi ABCD với \(AB = a,AC = {{2{\rm{a}}\sqrt 6 } \over 3}\). Trên đường thẳng vuông góc với mặt phẳng (P) tại giao điểm tại O của hai đường chéo hình thoi, ta lấy điểm S sao cho SB = a. Chứng minh rằng:
a) Tam giác ASC vuông.
b) Mặt phẳng (SAB) và mặt phẳng (SAD) vuông góc với nhau.
Lời giải chi tiết
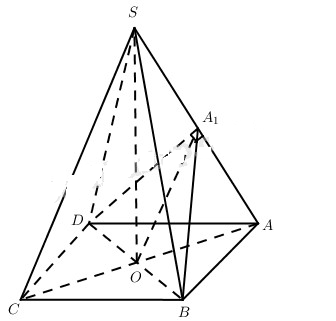
a) Ta có \(A{C^2} + B{{\rm{D}}^2} = 4{{\rm{a}}^2},AC = {{2{\rm{a}}\sqrt 6 } \over 3}\)
nên \(B{{\rm{D}}^2} = {{4{{\rm{a}}^2}} \over 3} \Rightarrow O{B^2} = {{{a^2}} \over 3}\)
Xét tam giác vuông SOB, ta có
\(S{O^2} = S{B^2} - O{B^2} = {{2{{\rm{a}}^2}} \over 3} \Rightarrow SO = {{a\sqrt 6 } \over 3}\)
Vậy tam giác SAC có trung tuyến SO bằng nửa AC nên SAC là tam giác vuông tại S.
b) Trong mặt phẳng (SOA) kẻ OA1 vuông góc với SA thì \(SA \bot mp\left( {{A_1}B{\rm{D}}} \right)\), từ đó \(\widehat {B{A_1}D}\) hoặc \({180^0} - \widehat {B{A_1}D}\), là góc giữa hai mặt phẳng (SAB) và (SAD).
Ta có
\(\eqalign{ & O{A_1} = {{OA.OS} \over {SA}} = {{OA.OS} \over {\sqrt {O{A^2} + O{S^2}} }} \cr & = {1 \over 2}.{{a\sqrt 6 } \over 3}.\sqrt 2 = {{a\sqrt 3 } \over 3} \cr} \)
Mặt khác \(B{\rm{D}} = {{2a\sqrt 3 } \over 3}\), từ đó \(\widehat {B{A_1}D} = {90^0}\) hay hai mặt phẳng (SAB) và (SAD) vuông góc.

