Cho hàm số f(x)=tan(πx).
LG a
Tìm tập xác định của hàm số y=f(x);
Lời giải chi tiết:
Hàm số y=tan(πx) xác định khi và chỉ khi cos(πx)≠0.
Mặt khác
cos(πx)=0
⇔πx=π2+kπ
⇔x=12+k(k∈Z)
Từ đó suy ra tập xác định của hàm số y=tan(πx) là: D=R∖{12+k|k∈Z}
LG b
Chứng minh rằng với mọi số nguyên k , ta có f(x+k)=f(x) . Từ đó suy ra y=f(x) là hàm số tuần hoàn với chu kì T = 1;
Lời giải chi tiết:
Với mọi k∈Z, ta có
f(x+k)=tan[π(x+k)]
=tan(πx+kπ)
=tan(πx)=f(x)
Trong các số nguyên dương, số 1 là nhỏ nhất.
Do đó tan(πx) là hàm số tuần hoàn với chu kì T=1.
LG c
Cho biết sự biến thiên của hàm số y=f(x) trên mỗi khoảng (−12+k;12+k),k∈Z;
Lời giải chi tiết:
Ta thấy
−12+k<x<12+k
⇔−π2+kπ<πx<π2+kπ
Từ đó suy ra hàm số tan(πx) đồng biến trên mỗi khoảng (−12+k;12+k),k∈Z
LG d
Vẽ đồ thị của hàm số đó.
Lời giải chi tiết:
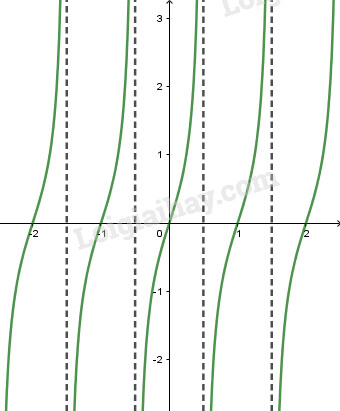
Đồ thị của hàm số có dạng như hình vẽ: