Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành, mặt bên SAB là tam giác vuông tại A. Với điểm M bất kì thuộc cạnh AD (M khác A và D), xét mặt phẳng (α) đi qua điểm M và song song với SA, CD.
a) Thiết diệm của hình chóp S.ABCD khi cắt bởi mp(α) là hình gì?
b) Tính diện tích thiết diện theo a và b; biết AB = a, SA = b, M là trung điểm của AD.
Lời giải chi tiết
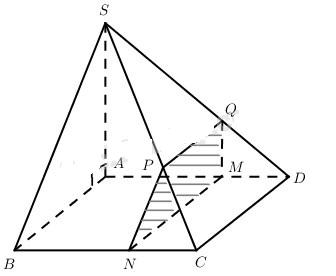
a) Dễ thấy thiết diện là tứ giác MNPQ trong đó MN // QP // CD, MQ // SA.
Do SA ⊥ AB, AB //MN, MQ // SA nên thiết diện MNPQ là hình thang vuông tại M.
b) \({S_{MNPQ}} = {1 \over 2}\left( {MN + PQ} \right).MQ\)
Do M là trung điểm của AD nên:
\(\eqalign{ & MQ = {1 \over 2}SA = {1 \over 2}b \cr & PQ = {1 \over 2}CD = {1 \over 2}a \cr & MN = a \cr} \)
Vậy \({S_{MNPQ}} = {1 \over 2}\left( {a + {a \over 2}} \right).{b \over 2} = {{3{\rm{a}}b} \over 8}\).

