Đề bài
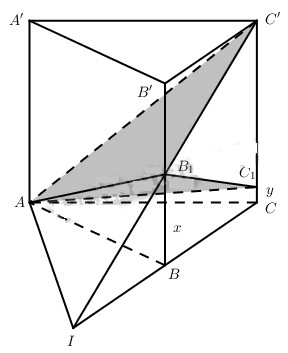
Cho hình lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a. Lấy điểm B1 thuộc BB’, điểm C1 thuộc CC’. Đặt BB1=x,CC1=y.
a) Tam giác AB1C1 có thể vuông ở A được không? Tìm hệ thức liên hệ giữa a, x, y để AB1C1 là tam giác vuông tại B1.
b) Giả sử AB1C1 là tam giác thường và B1 là trung điểm của BB’, y = 2x và α là góc giữa mp(ABC) và mp(AB1C1). Hãy tính diện tích tam giác AB1C1 và độ dài cạnh bên của hình lăng trụ đã cho.
Lời giải chi tiết
a) ● Tam giác AB1C1 vuông ở A khi và chỉ khi
B1C21=AB21+AC21
Mặt khác
B1C21=a2+(x−y)2AB21=a2+x2AC21=a2+y2
Do đó tam giác AB1C1 vuông ở A khi và chỉ khi
a2+(x−y)2=2a2+x2+y2⇔2xy=−a2
Điều này không xảy ra. Vậy tam giác AB1C1 không thể vuông tại A được.
● Tam giác AB1C1 vuông tại B1 khi và chỉ khi
AC21=AB21+B1C21⇔a2+y2=a2+x2+a2+(x−y)2⇔2xy=2x2+a2
Đó là hệt thức liên hệ giữa a, x, y để tam giác AB1C1 vuông tại B1.
b) Khi B1 là trung điểm của BB’, y = 2x thì C1 trùng với C’.
Gọi I=BC∩B1C′ thì AI=(AB1C′)∩(ABC).
Vì B1B=12BB′ nên BI = BC, từ đó ta có IAC là tam giác vuông tại A, tức là AC⊥AI.
Mặt khác, C′C⊥(ABC) nên AC′⊥AI (định lí ba đường vuông góc).
Như vậy ^C′AC là góc giữa mp(AB1C’) và mp(ABC).
Theo giả thiết thì ^C′AC=α
Từ đó SABC=SAB1C1cosα
tức là SAB1C1=SABCcosα
Như vậy SAB1C1=a2√34cosα
Ta có: CC′=ACtanα=atanα
Vậy độ dài cạnh bên của hình lăng trụ đã cho là atanα.
