Đề bài
Cho tam giác đề ABC có chiều cao AH = 5a. Điểm O thuộc đoạn thẳng AH sao cho AO = a. Điểm S trên đường thẳng vuông góc với mặt phẳng (ABC) tại O và SO = 2a.
a) Chứng mịn AS và CS vuông góc với nhau. Tính góc giữa hai đường thẳng AB và SC.
b) Gọi I là trung điểm của OH; (α) là mặt phẳng đi qua điểm I và vuông góc với AH. Thiết diện của hình chóp S.ABC khi cắt bởi (α) là hình gì? Tính diện tích thiết diện.
Lời giải chi tiết
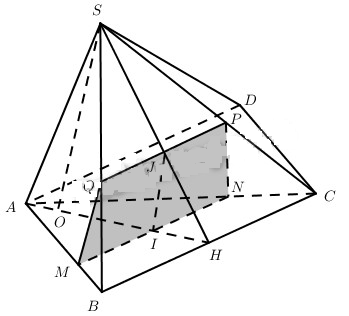
a) Dễ thấy
BC=10a√3SA2=SO2+AO2=4a2+a2=5a2SC2=SO2+AO2=4a2+16a2+25a23=85a23AC2=100a23
Ta có SA2+SC2=AC2
Vậy SA⊥SC.
+ Kẻ AD song song và bằng BC (hai tia AD, BC cùng chiều) thì góc giữa AB và SC chính là góc giữa CD và SC, đó là ^SCD hoặc 1800−^SCD.
Dễ thấy SA⊥BC, do AD // BC nên SA⊥AD, tức là tam giác SAD vuông.
Do đó SD2=SA2+AD2=5a2+100a23=115a23,
mặt khác SD2=SC2+DC2−2SC.DCcos^SCD
nên ta có
115a23=85a23+100a23−2.a√85√3.10a√3cos^SCD⇒cos^SCD=72√85
Vậy góc giữa AB và SC là α mà
cosα=72√85.
Do (α)⊥AH,SO⊥AH và BC⊥AH nên SO và BC cùng song song với (α). Khi đó (α)∩(ABC)=MN, MN qua I và MN // BC
(α)∩(SOH)=IJ,IJ//SO(α)∩(SBC)=PQ
PQ qua J và PQ // BC.
Dễ thấy MNPQ là hình thang cân với chiều cao JI.
Ta có :
IJ=12SO=aPQ=12BC=5a√3MNBC=3a5a⇒MN=10a.3√3.5=2a√3.
Suy ra
SMNPQ=12(MN+PQ).IJ=12(2a√3+5a√3).a=11a22√3

