Bài 7
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) Tam giác có trục đối xứng;
(B) Tứ giác có trục đối xứng;
(C) Hình thang có trục đối xứng;
(D) Hình thang cân có trục đối xứng.
Lời giải chi tiết:
Đáp án: D
Hình thang cân có 1 trục đối xứng (đường thẳng đi qua trung điểm hai cạnh đáy)
Bài 8
Trong các hình dưới đây hình nào có ba trục đối xứng?
(A) Đoạn thẳng; (B) Đường tròn;
(C) Tam giác đều; (D) Hình vuông.
Lời giải chi tiết:
Đáp án: C
Tam giác đều có 3 trục đối xứng, đó chính là 3 đường cao.
Ngoài ra, đoạn thẳng có 2 trục đối xứng (đường trung trực và đường thẳng chứa đoạn thẳng đó)
Đường tròn có vô số trục đối xứng (đường kính)
Hình vuông có 4 trục đối xứng (2 đường chéo, 2 đường thẳng đi qua trung điểm các cạnh đối diện).
Bài 9
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) Tam giác đều có tâm đối xứng;
(B) Tứ giác có tâm đối xứng;
(C) Hình thang cân có tâm đối xứng;
(D) Hình bình hành có tâm đối xứng.
Lời giải chi tiết:
Đáp án: D
Tam giác đều không có tâm đối xứng (A sai)
Tứ giác bất kì chưa chắc có tâm đối xứng (B sai)
Hình thang cân không có tâm đối xứng (C sai)
Hình bình hành có tâm đối xứng là giao điểm hai đường chéo (D đúng)
Bài 10
Cho hai đường thẳng bất kì d và d’. Có bao nhiêu phép quay biến đường thẳng d thành đường thẳng d’?
(A) Không có phép nào;
(B) Có một phép duy nhất;
(C) Chỉ có hai phép;
(D) Có vô số phép.
Lời giải chi tiết:
Đáp án: D
Có vô số phép quay biến d thành d’.
Bài 11
Cho tam giác đều ABC với O là tâm đường tròn ngoại tiếp. Với giá trị nào dưới đây của \(\varphi \) thì phép quay \({Q_{\left( {O;\varphi } \right)}}\) biến tam giác đều ABC thành chính nó?
(A) \(\varphi = {\pi \over 3}\) ; (B) \(\varphi = {{2\pi } \over 3}\) ;
(C) \(\varphi = {{3\pi } \over 2}\) ; (D) \(\varphi = {\pi \over 2}.\)
Lời giải chi tiết:
Đáp án: B
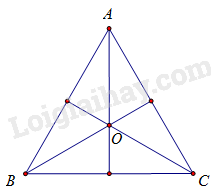
Ta có:
\(\begin{array}{l}{Q_{\left( {O;\frac{{2\pi }}{3}} \right)}}\left( A \right) = B\\{Q_{\left( {O;\frac{{2\pi }}{3}} \right)}}\left( B \right) = C\\{Q_{\left( {O;\frac{{2\pi }}{3}} \right)}}\left( C \right) = A\\ \Rightarrow {Q_{\left( {O;\frac{{2\pi }}{3}} \right)}}\left( {ABC} \right) = ABC\end{array}\)
Bài 12
Trong các phép sau đây, phép nào có tính chất: Biến mỗi đường thẳng a thành đường thẳng a’ không song song với a?
(A) Phép tịnh tiến;
(B) Phép đối xứng trục;
(C) Phép đối xứng tâm;
(D) Phép quay với góc quay \({\pi \over 2}\).
Lời giải chi tiết:
Đáp án: D
Phép quay với góc quay \({\pi \over 2}\) biến đường thẳng a thành đường thẳng a’ vuông góc với a nên chắc chắn chúng không song song.
Bài 13
Hợp thành của hai phép đối xứng trục có trục song song là phép nào trong các phép sau đây?
(A) Phép đối xứng trục;
(B) Phép đối xứng tâm;
(C) Phép quay;
(D) Phép tịnh tiến.
Lời giải chi tiết:
Đáp án: D
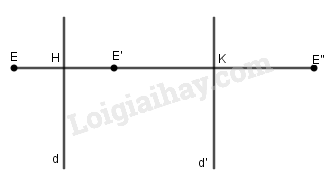
Xét hai trục \(d//d'\). Ta có:
\({D_d}\left( E \right) = E'\) \( \Rightarrow \overrightarrow {EE'} = 2\overrightarrow {HE'} \)
\({D_{d'}}\left( {E'} \right) = E''\) \( \Rightarrow \overrightarrow {E'E''} = 2\overrightarrow {E'K} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {EE''} = \overrightarrow {EE'} + \overrightarrow {E'E''} \\ = 2\overrightarrow {HE'} + 2\overrightarrow {E'K} \\ = 2\left( {\overrightarrow {HE'} + \overrightarrow {E'K} } \right)\\ = 2\overrightarrow {HK} \\ \Rightarrow E'' = {T_{\overrightarrow {HK} }}\left( E \right)\end{array}\)
Vậy hợp thành của hai phép đối xứng trục có các trục song song là một phép tịnh tiến.
Bài 14
Hợp thành của hai phép đối xứng trục có trục cắt nhau là phép nào trong các phép sau đây?
(A) Phép đối xứng trục;
(B) Phép quay
(C) Phép tịnh tiến;
(D) Phép đồng nhất.
Lời giải chi tiết:
Đáp án: B
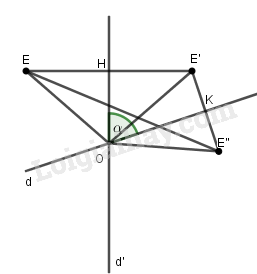
Xét hai trục đối xứng \(d,d'\) cắt nhau tại \(O\) và góc \(\left( {d,d'} \right) = \alpha \)
Ta có:
\(\begin{array}{l}{D_d}\left( E \right) = E' \Rightarrow OE = OE'\\{D_{d'}}\left( {E'} \right) = E'' \Rightarrow OE' = OE''\\ \Rightarrow OE = OE''\end{array}\)
Lại có:
\(\begin{array}{l}\widehat {EOE''} = \widehat {EOE'} + \widehat {E'OE''}\\ = 2\widehat {HOE'} + 2\widehat {E'OK}\\ = 2\left( {\widehat {HOE'} + \widehat {E'OK}} \right)\\ = 2\widehat {HOK}\\ = 2\alpha \\ \Rightarrow \widehat {EOE''} = 2\alpha \end{array}\)
Vậy hợp thành của hai phép đối xứng trục qua đường thẳng \(d,d'\) ta được phép quay tâm \(O\).

