Đề bài
Hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mp(ABCD) và SA = a.
a) Gọi D1 là trung điểm của SD. Chứng minh rằng \(A{{\rm{D}}_1} \bot \left( {SC{\rm{D}}} \right)\).
b) Gọi O là tâm của hình vuông ABCD, M là điểm thay đổi trên SD. Chứng minh rằng hình chiếu của điểm O trên CM thuộc đường tròn cố định.
Lời giải chi tiết
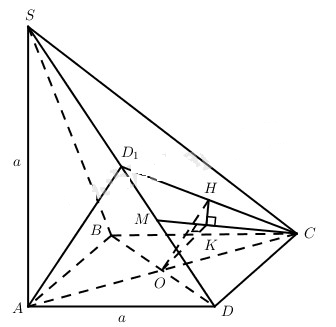
a) Vì SA = AD = a và D1 là trung điểm của SD nên \(A{{\rm{D}}_1} \bot S{\rm{D}}\). Mặt khác, ta có \(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\) nên \(A{{\rm{D}}_1} \bot C{\rm{D}}.\)
Vậy \(A{{\rm{D}}_1} \bot \left( {SC{\rm{D}}} \right).\)
b) Kẻ OH // AD1 thì H là trung điểm của D1C và \(OH \bot \left( {SC{\rm{D}}} \right)\), ngoài ra H cố định.
Gọi K là hình chiếu của O trên CM thì HK ⊥ KC (định lí ba đường vuông góc). Từ đó, suy ra điểm K thuộc đường tròn đường kính HC trong mp(SCD). Đó là đường tròn cố định chứa hình chiếu của tâm hình vuông trên mặt phẳng (SCD).

