Đề bài
Cho hình hộp ABCD.A’B’C’D’. Gọi D1,D2,D3 lần lượt là điểm đối xứng của điểm D’ qua A, B’, C. Chứng tỏ rằng B là trọng tâm của tứ diện D1D2D3D′.
Lời giải chi tiết
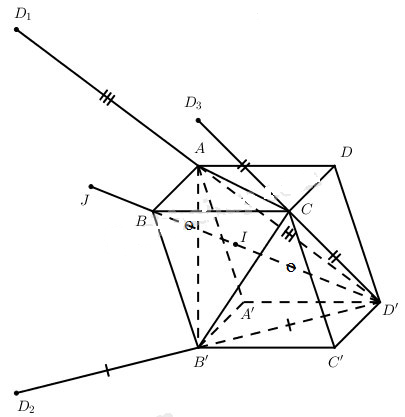
Cách 1.
Đặt →AA′=→a,→AB=→b,→AD=→c
Từ giả thiết, ta có
→BD′+→BD1=2→BA=−2→b
mà →BD′=→a−→b+→c
Vậy →BD1=−→a−→b−→c.
Lập luận tương tự như trên, ta có →BD2=→a+→b−→c và →BD3=−→a+→b+→c
Vậy →BD1+→BD2+→BD3+→BD′=→0
Điều này chứng tỏ B là trọng tâm của tứ diện D1D2D3D′ .
Cách 2.
Gọi I là giao điểm của BD’ và mp(AB’C) thì D’I = 2IB.
Gọi J là giao điểm của BD’ với mp (D1D2D3), do D1, D2, D3 là các điểm đối xứng của D’ lần lượt qua A, B’, C nên IJ = ID’ hay D′B=34D′J.
Mặt khác I là trọng tâm tam giác AB’C nên J là trọng tâm tam giác D1D2D3. Từ đó B là trọng tâm của tứ diện D1D2D3D′.

