Đề bài
Cho tứ diện ABCD. Một mặt phẳng (P) di động luôn song song với AB và CD lần lượt cắt các cạnh AC, AD, BD, BC tại M, N, E, F.
a) Chứng minh rằng tứ giác MNEF là một hình bình hành.
b) Tìm tập hợp tâm I của hình bình hành MNEF.
Lời giải chi tiết
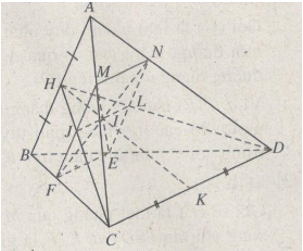
a) Ta có:
\(\eqalign{
& AB//\left( P \right),\,AB \subset \left( {ABC} \right) \cr
& \Rightarrow \left( {ABC} \right) \cap \left( P \right) = MF//AB \cr} \)
Và
\(\eqalign{
& AB//\left( P \right),\,AB \subset \left( {ABD} \right) \cr
& \Rightarrow \left( {ABD} \right) \cap \left( P \right) = NE//AB. \cr} \)
Vậy MF//NE//AB.
Chứng minh tương tự ta có: MN//EF//CD.
Từ (1) và (2) suy ra tứ giác MNEF là hình bình hành.
b) Gọi H và K lần lượt là trung điểm của AB và CD.
Gọi J và L lần lượt là các giao điểm của các cặp đường thẳng CH và MF, DH và NE thì rõ ràng ba điểm J, I, L thẳng hàng. Vậy khi (P) di động thì tâm I của hình bình hành MNEF chạy trên đoạn thẳng HK.
Ngược lại, lấy một điểm I bất kì trên đoạn HK. Qua I kẻ đường thẳng song song với CD lần lượt cắt CH và DH tại J và L. Qua J và L lần lượt kẻ hai đường thẳng MF (\(\left( {M \in AC,F \in BC} \right),\,NE\left( {N \in AD,\,E \in BD} \right)\) cùng song song với AB. Dễ thấy tứ giác MNEF là hình bình hành và có tâm I. Vậy tập hợp tâm I của hình bình hành MNEF là đoạn thẳng HK.

