Đề bài
Trong mp(P) cho hai đường thẳng a và b cắt nhau tại O. Hai điểm A, B nằm ngoài mp(P) và đường thẳng AB cắt mp(P) tại C sao cho \(C \notin a,\,C \notin b.\) Một mặt phẳng (Q) thay đổi luôn đi qua AB và cắt hai đường thẳng a, b lần lượt tại \({A_1}\) và \({B_1}\)
a) Chứng minh rằng đường thẳng \({A_1}{B_1}\) luôn đi qua một điểm cố định.
b) Gọi I là giao điểm của \(A{A_1}\) và \(B{B_1}\), J là giao điểm của \(A{B_1}\) và \(B{A_1}.\) Chứng minh rằng mỗi điểm I và J chạy trên một đường thẳng cố định.
c) Chứng minh rằng đường thẳng IJ luôn đi qua một điểm cố định.
Lời giải chi tiết
a) Mặt phẳng (Q) và mặt phẳng (P) có ba điểm chung là \({A_1},\,{B_1}\) và C nên ba điểm đó phải thẳng hàng; tức là đường thẳng \({A_1}{B_1}\) luôn đi qua điểm cố định C.
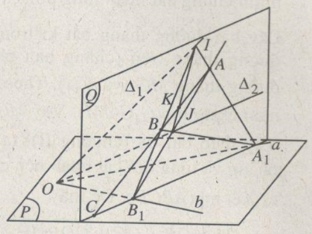
b) Ta có:
\(\eqalign{
& \left. \matrix{
I \in A{A_1} \hfill \cr
A{A_1} \subset mp\left( {A,\,a} \right) \hfill \cr} \right\} \Rightarrow I \in mp\left( {A,\,a} \right) \cr
& \left. \matrix{
I \in B{B_1} \hfill \cr
B{B_1} \subset mp\left( {B,\,b} \right) \hfill \cr} \right\} \Rightarrow I \in mp\left( {B,\,b} \right). \cr} \)
Từ đó, suy ra I thuộc giao tuyến \({\Delta _1}\) của hai mặt phẳng (B, b) và (A, a). Do hai mặt phẳng này cố định nên đường thẳng \({\Delta _1}\) cố định.
Chứng minh tương tự, điểm J chạy trên đường thẳng cố định \({\Delta _2}\) là giao tuyến của hai mặt phẳng cố định mp(A, b) và mp(B, a). Chú ý \({\Delta _1},\,{\Delta _2}\) đều đi qua O).
c) Hai đường thẳng IJ, AB đều thuộc mp(Q) và chúng không thể song song nên chúng cắt nhau tại một điểm K.
Ta có:
\(\left. \matrix{
K \in IJ \hfill \cr
IJ \subset mp\left( {{\Delta _1},\,{\Delta _2}} \right) \hfill \cr} \right\} \Rightarrow K \in mp\left( {{\Delta _1},\,{\Delta _2}} \right).\)
Mặt khác K thuộc AB. Do đó K chính là giao điểm của đường thẳng cố định AB với \(mp\left( {{\Delta _1},\,{\Delta _2}} \right)\) cố định nên K cố định.
Vậy đường thẳng IJ luôn đi qua điểm K cố định.

