Đề bài
Cho hai đường thẳng a, b phân biệt và điểm C không nằm trên chúng. Hãy xác định hai điểm A, B lần lượt nằm trên a và b sao cho tam giác ABC là tam giác đều.
Lời giải chi tiết
Giả sử đã dựng tam giác đều ABC thỏa mãn điều kiện cho. Khi đó, góc \(\left( {CA,CB} \right) = \pm{60^o}.\)
Nếu \(\left( {CA,CB} \right) = {60^o}\) thì phép quay Q tâm C góc quay \({60^o}\) sẽ biến A thành B và biến đường thẳng a thành đường thẳng a’ đi qua B.
Vậy ta có thể xác định điểm B như sau:
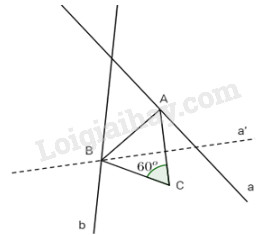
Dựng đường thẳng a’ là ảnh của đường thẳng a qua phép quay Q, rồi lấy giao điểm B của a’ và b.
Điểm A được xác định như là ảnh của B qua phép quay tâm C góc quay \( - {60^o}.\)
Làm tương tự cho trường hợp \(\left( {CA,CB} \right) = - {60^o}.\)
Bài toán có ít nhất một nghiệm hình, có thể có vô số nghiệm hình.

