Đề bài
Cho hình chóp S.ABCD có đáy là hình thoi, đường chéo AC = 4a, đường chéo BD = 2a; O là giao điểm của AC với BD và SO vuông góc với mặt phẳng (ABC), SO = h. Một mặt phẳng (α) đi qua điểm A và vuông góc với đường thẳng SC tại điểm C1. Tìm hệ thức liên hệ giữa a và h để điểm C1 nằm trong đoạn thẳng SC, C1 khác S và khác C. Khi đó, tính diện tích thiết diện của hình chóp S.ABCD cắt bởi mp(α).
Lời giải chi tiết
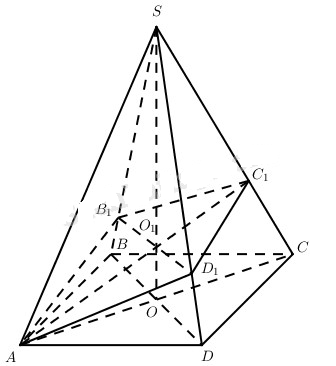
Vì \(\left( \alpha \right) \bot SC\) và \(A \in \left( \alpha \right)\) nên \(A{C_1} \bot SC\). Mặt khác, gọi \({B_1}{D_1} = \left( \alpha \right) \cap \left( {SBD} \right)\) thì B1D1 song song với BD và B1D1 qua \({O_1} = A{C_1} \cap SO\) (do \(B{\rm{D}} \bot SC,\left( \alpha \right) \bot SC\) nên BD // (α)).
Vì SAC là tam giác cân tại S và \(A{C_1} \bot SC\) nên C1 thuộc SC khi và chỉ khi \(\widehat {ASC} < {90^0}\) tức là \(\widehat {OSC} < {45^0}\). Xét tam giác vuông SOC, điều kiện \(\widehat {OSC} < {45^0}\) tương đương với \(SO > OC = {{AC} \over 2} = 2a\). Vậy để C1 thuộc SC, C1 không trùng với C và S thì hệ thức liên hệ giữa h và a là h > 2a.
Dễ thấy thiết diện của S.ABCD khi cắt bởi (α) là tứ giác AB1C1D1 có tính chất \(A{C_1} \bot {B_1}{D_1}\) . Do đó \({S_{A{B_1}{C_1}{D_1}}} = {1 \over 2}A{C_1}.{B_1}{D_1}\).
Ta có:
\(\eqalign{ & A{C_1}.SC = SO.AC \Rightarrow A{C_1} = {{4{\rm{a}}h} \over {\sqrt {4{{\rm{a}}^2} + {h^2}} }}; \cr & {{{B_1}{D_1}} \over {B{\rm{D}}}} = {{S{O_1}} \over {SO}}, \cr} \)
mặt khác
\(\eqalign{ & {{{O_1}O} \over {CO}} = {{AO} \over {SO}} \cr & \Rightarrow {O_1}O = {{4{{\rm{a}}^2}} \over h} \cr & \Rightarrow S{O_1} = {{{h^2} - 4{a^2}} \over h} \cr} \)
Từ đó \({{{B_1}{D_1}} \over {B{\rm{D}}}} = {{{h^2} - 4{{\rm{a}}^2}} \over {{h^2}}}\)
hay \({B_1}{D_1} = {{2{\rm{a}}\left( {{h^2} - 4{{\rm{a}}^2}} \right)} \over {{h^2}}}\)
Vậy
\(\eqalign{ & {S_{A{B_1}{C_1}{D_1}}} = {1 \over 2}.{{4{\rm{a}}h} \over {\sqrt {4{{\rm{a}}^2} + {h^2}} }}.{{2{\rm{a}}\left( {{h^2} - 4{{\rm{a}}^2}} \right)} \over {{h^2}}} \cr & = {{4{{\rm{a}}^2}\left( {{h^2} - 4{{\rm{a}}^2}} \right)} \over {h\sqrt {4{{\rm{a}}^2} + {h^2}} }} \cr} \)

