Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt đáy SA = a. Tính:
a) Khoảng cách từ điểm S đến mp(A1CD) trong đó A1 là trung điểm của SA;
b) Khoảng cách giữa AC và SD.
Lời giải chi tiết
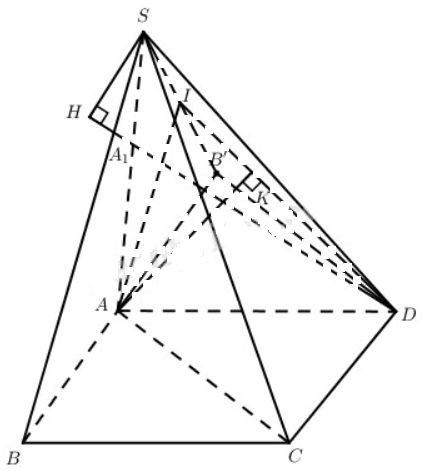
a) Ta có \(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\) nên \(\left( {C{\rm{D}}{A_1}} \right) \bot \left( {SA{\rm{D}}} \right)\). Từ đó, khi kẻ đường cao SH của tam giác SA1D thì:
\(SH \bot mp\left( {C{\rm{D}}{A_1}} \right)\).
và \(SH = d\left( {S;mp\left( {C{\rm{D}}{A_1}} \right)} \right)\).
Ta có
\(\eqalign{ & SH.{A_1}D = 2{{\rm{S}}_{S{A_1}D}} = {S_{SA{\rm{D}}}} = {{{a^2}} \over 2} \cr & {A_1}D = \sqrt {{a^2} + {{{a^2}} \over 4}} = {{a\sqrt 5 } \over 2} \cr} \)
Vậy \(SH = {{{a^2}} \over 2}.{2 \over {a\sqrt 5 }} = {a \over {\sqrt 5 }} = {{a\sqrt 5 } \over 5}.\)
Kẻ qua D đường thẳng song song với AC, cắt đường thẳng AB tại B', khi đó \(B'D = a\sqrt 2 ,AB' = a,SB' = a\sqrt 2 ,S{\rm{D}} = a\sqrt 2 \).
Vậy SB’D là tam giác đều. Gọi I là trung điểm của SB’ thì:
\(DI = {{a\sqrt 6 } \over 2},SB' \bot \left( {AI{\rm{D}}} \right)\).
từ đó \(\left( {AI{\rm{D}}} \right) \bot \left( {SB'D} \right)\).
Vậy khi kẻ đường cao AK của tam giác AID thì AK là khoảng cách từ A đến mp(SB’D). Mặt khác AC // (SB’D) nên AK cũng là khoảng cách giữa AC và SD.
Ta có \({\rm{AI = }}{{a\sqrt 2 } \over 2},A{\rm{D}} = a\)
Vì \(A{\rm{D}} \bot \left( {SAB} \right)\) nên \(A{\rm{D}} \bot AI\).
Do đó \(AK = {{AI.A{\rm{D}}} \over {DI}} = {{{{a\sqrt 2 } \over 2}.a} \over {{{a\sqrt 6 } \over 2}}} = {a \over {\sqrt 3 }}\).
Vậy khoảng cách giữa AC và SD bằng \({{a\sqrt 3 } \over 3}\).

