Đề bài
Cho tứ diện ABCD và bốn điểm M, N, E, F lần lượt nằm trên các cạnh AB, BC, CD và DA. Chứng minh rằng:
a) Nếu bốn điểm M, N, E, F đồng phẳng thì \({{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{FD} \over {FA}} = 1\).
b) Nếu \({{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{FD} \over {FA}} = 1\) thì bốn điểm M, N, E, F đồng phẳng.
Lời giải chi tiết
a) Trường hợp 1. MN // EF
Theo hệ quả của định lí giao tuyến của ba mặt phẳng (ABC), (ACD), (MNEF) ta có MN//EF // AC. Do đó ta có:
\({{MA} \over {MB}} = {{NC} \over {NB}},\,{{EC} \over {ED}} = {{FA} \over {FD}}\)
\(\eqalign{
& \Rightarrow {{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{FD} \over {FA}} \cr
& = {{NC} \over {NB}}. {{NB} \over {NC}}.{{FA} \over {FD}}.{{FD} \over {FA}} = 1 \cr} \) suy ra điều phải chứng minh.
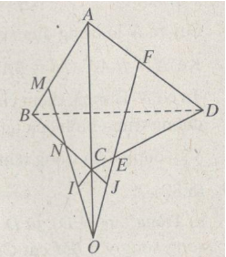
Trường hợp 2. MN cắt EF tại O.
Theo định lí về giao tuyến của ba mặt phẳng (ABC), (ADC), (MNEF) ta có MN, AC, EF đồng quy tại O. Kẻ \(CI//AB,\,CJ//AD\,\left( {I \in MN,\,J \in FE} \right),\) ta có:
\(\eqalign{
& {{NB} \over {NC}} = {{MB} \over {CI}},\,{{OC} \over {OA}} = {{CI} \over {MA}} \cr
& \Rightarrow {{MA} \over {MB}}.{{NB} \over {NC}}.{{OC} \over {OA.}} \cr
& = {{MA} \over {MB}}.{{MB} \over {CI}}.{{CI} \over {MA}} = 1 \cr} \)
Tương tự ta có:
\({{EC} \over {ED}}.{{FD} \over {FA}}.{{OA} \over {OC}} = 1\)
Vậy \({{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{FD} \over {FA}} = {{OA} \over {OC}}.{{OC} \over {OA}} = 1\)
b) Giả sử mặt phẳng (MNE) cắt cạnh AD tại F’. Theo câu a), ta có:
\({{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{F'D} \over {F'A}} = 1\)
Theo giả thiết \({{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{FD} \over {FA}} = 1 \Rightarrow F'D = FD\).
Vì F, F’ đều nằm trong đoạn thẳng AD nên \(F' \equiv F\) . Điều này có nghĩa là bốn điểm M, N, E, F đồng phẳng.

