Đề bài
Cho hai hình chữ nhật ABCD, ABEF nằm trên hai mặt phẳng khác nhau sao cho hai đường chéo AC và BF vuông góc. Gọi CH và FK lần lượt là hai đường cao của hai tam giác BCE và ADF. Chứng minh rằng:
a) ACH và BFK là các tam giác vuông.
b) \(BF \bot AH\) và \(AC \bot BK\).
Lời giải chi tiết
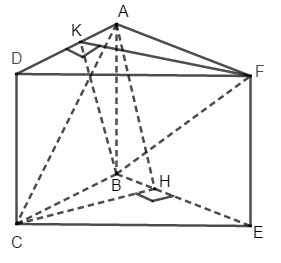
a) Ta có:
\(\left. \matrix{ AB \bot \left( {BCE} \right) \hfill \cr CH \bot BE \hfill \cr} \right\} \Rightarrow CH \bot AH\)
Vậy ACH là hình tam giác vuông tại H.
\(\left. \matrix{ AB \bot \left( {ADF} \right) \hfill \cr FK \bot AD \hfill \cr} \right\} \Rightarrow FK \bot KB\)
Vậy FKB là hình tam giác vuông tại K.
b) Ta có:
\(\left. \matrix{ CH \bot BE \hfill \cr CH \bot AB \hfill \cr} \right\} \Rightarrow CH \bot BF\)
Mặt khác \(AC \bot BF\)
Vậy \(BF \bot AH\)
Tương tự, ta có \(AC \bot BK\).

