Đề bài
Cho hình chóp tứ giác S.ABCD; \(\Delta \) là một đường thẳng nằm trong mp(ABCD) sao cho \(\Delta \) song song với BD, M là trung điểm cạnh SA. Hãy xác định thiết diện của hình chóp S.ABCD khi cắt bởi mp(M, \(\Delta \)) trong các trường hơp sau đây:
a) \(\Delta \) không cắt cạnh nào của đáy ABCD.
b) \(\Delta \) đi qua điểm C.
c) \(\Delta \) cắt hai cạnh BC và CD tại hai điểm I và J.
d) \(\Delta \) cắt hai cạnh AB và AD tại hai điểm I’ và J’.
Lời giải chi tiết
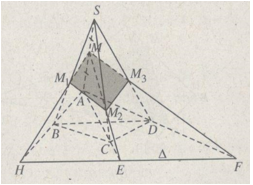
a) Gọi H, E, F lần lượt là các giao điểm của \(\Delta \) với các đường thẳng AB, AC và AD. Khi đó các cạnh bên SB, SC, SD của hình chóp lần lượt cắt các đường thẳng MH, ME và MF tại \({M_1};\,{M_2};\,{M_3}.\) Thiết diện của hình chóp khi cắt bởi \(mp\left( {M,\Delta } \right)\) trong trường hợp này là tứ giác \(M{M_1}{M_2}{M_3}.\)
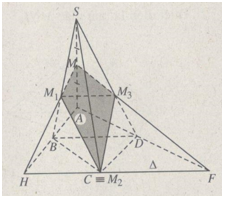
b) Thiết diện là tứ giác \(M{M_1}C{M_3}.\)
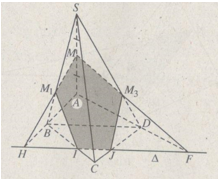
c) Thiết diện là ngũ giác \(M{M_1}IJ{M_3}.\)
d) Thiết diện là tam giác \(MI'J'.\)