Đề bài
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M, I, J, O lần lượt là trung điểm của SD, AB, CD, IJ.
a) Chứng minh rằng nếu \({G_1},\,{G_2}\) lần lượt là trọng tâm của tam giác SAB và ABC thì \({G_1}{G_2}//MJ.\)
b) Chứng minh rằng tâm đường thẳng mà mỗi đường thẳng đi qua trung điểm của một cạnh hình chóp và trọng tâm của tam giác tạo bởi ba đỉnh hình chóp không nằm trên cạnh nói trên đồng quy tại một điểm G.
c) Chứng minh rằng điểm G nằm trên đoạn thẳng SO và GS = 4GO.
Lời giải chi tiết
a) Ta có:
\({{I{G_1}} \over {IS}} = {{I{G_2}} \over {IC}} = {1 \over 3} \Rightarrow {G_1}{G_2}//SC\)
Mặt khác MJ là đường trung bình của tam giác DSC nên MJ//SC. Từ đó, suy ra \({G_1}{G_2}//MJ.\)
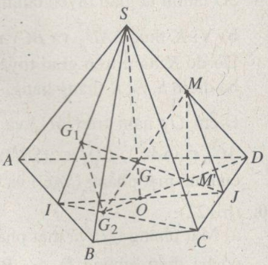
b) Rõ ràng tám đường thẳng đã cho không đồng phẳng; ta chỉ cần chứng minh chúng cắt nhau từng đôi.
Lấy hai đường thẳng bất kì trong tám đường thẳng trên (chẳng hạn như hai đường thẳng \(M{G_2}\) và \(J{G_1}\)). Theo câu a) thì \({G_1}{G_2}//MJ,\) do đó \(M{G_2}\) và \(J{G_1}\) cắt nhau.
Vậy theo bài 68 (chương II), ta có tám đường thẳng đã cho không đồng phẳng và từng đôi cắt nhau nên chúng đồng quy tại một điểm G.
c) Xét mp(ABCD). Dễ thấy:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {OD} = - \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = - 3\overrightarrow {O{G_2}} \) (vì \({G_2}\) là trọng tâm tam giác ABC)
\( \Rightarrow O,\,{G_2},\,D\) thẳng hàng và \(OD = 3O{G_2}\)
Xét ba mặt phẳng \(\left( {{G_1}{G_2}JM} \right),\,\left( {{G_2}MD} \right),\,\left( {SIJ} \right).\) Ta có:
\(\eqalign{
& \left( {{G_1}{G_2}JM} \right) \cap \left( {{G_2}MD} \right) = {G_2}M \cr
& \left( {{G_1}{G_2}JM} \right) \cap \left( {SIJ} \right) = {G_1}J \cr
& \left( {{G_2}MD} \right) \cap \left( {SIJ} \right) = SO. \cr} \)
Vậy \({G_2}M,\,{G_1}J\) và SO đồng quy. Theo kết quả câu b) thì \({G_2}M\) và \({G_1}J\) cắt nhau tại G. Vậy điểm G nằm trên SO.
Kẻ MM’ song song với SO và cắt \({G_2}D\) tại M’, ta có:
\(OM' = M'D = {1 \over 2}OD = {3 \over 2}O{G_2}\)
và \({{OG} \over {MM'}} = {{O{G_2}} \over {{G_2}M'}} = {{O{G_2}} \over {{5 \over 2}O{G_2}}} = {2 \over 5}\)
\(\eqalign{
& \Rightarrow OG = {2 \over 5}MM' = {1 \over 5}SO \cr
& \Rightarrow GS = 4GO. \cr} \)

