Đề bài
Cho tứ diện ABCD có cạnh AD vuông góc với mp(DBC). Gọi AE, BF là hai đường cao của tam giác ABC; H và K lần lượt là trực tâm của tam giác ABC và tam giác DBC. Chứng minh rằng:
a) \(mp\left( {A{\rm{D}}E} \right) \bot mp\left( {ABC} \right)\) và \(mp\left( {BFK} \right) \bot mp\left( {ABC} \right)\).
b) \(HK \bot mp\left( {ABC} \right)\)
Lời giải chi tiết
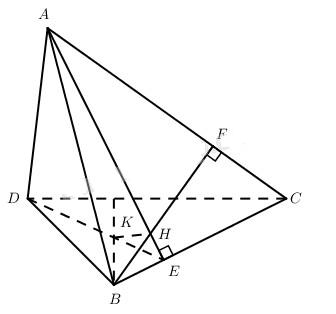
a) Vì \(A{\rm{D}} \bot \left( {DBC} \right)\) nên \(A{\rm{D}} \bot BC\).
Mặt khác \(A{\rm{E}} \bot BC\). Vậy \(BC \bot \left( {A{\rm{D}}E} \right)\), từ đó ta có \(\left( {ABC} \right) \bot \left( {A{\rm{D}}E} \right)\).
Vì K là trực tâm tam giác DBC nên \(BK \bot AC\). Theo giả thiết \(A{\rm{D}} \bot \left( {DBC} \right)\), vậy \(BK \bot AC\) (định lí ba đường vuông góc). Kết hợp với \(BF \bot AC\) ta có \(AC \bot \left( {BFK} \right)\), từ đó \(mp\left( {ABC} \right) \bot mp\left( {BFK} \right)\).
b) Từ câu a), ta có
\(\eqalign{ & mp\left( {BFK} \right) \bot mp\left( {ABC} \right) \cr & mp\left( {A{\rm{D}}E} \right) \bot mp\left( {ABC} \right) \cr & HK = mp\left( {A{\rm{D}}E} \right) \cap mp\left( {BFK} \right) \cr} \)
Vậy \(HK \bot mp\left( {ABC} \right)\).

