Đề bài
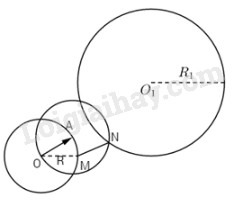
Cho hai đường tròn không đồng tâm (O; R) và (O1;R1) và một điểm A trên (O; R). Xác định điểm M trên (O; R) và điểm N trên (O1;R1) sao cho →MN=→OA.
Lời giải chi tiết
Giả sử đã xác định được M và N theo yêu cầu của bài toán.
Khi đó, phép tịnh tiến T theo vecto →OA sẽ biến điểm M thành điểm N và biến đường tròn (O; R) thành đường tròn (A; R).
Vì (O; R) đi qua M, nên (A; R) đi qua N.
Do đó N là giao điểm của hai đường tròn (A; R) và (O1;R1).
Từ đó dễ dàng suy ra cách dựng.
Số nghiệm hình phụ thuộc vào số giao điểm của hai đường tròn (A; R) và (O1;R1).