Đề bài
Cho ba đường thẳng đôi một chéo nhau không cùng song song với một mặt phẳng và một điểm G không nằm trên bất cứ đường nào trong ba đường thẳng đó. Hãy dựng tam giác có các đỉnh thứ tự nằm trên ba đường thẳng đã cho và nhận G làm trọng tâm
Lời giải chi tiết
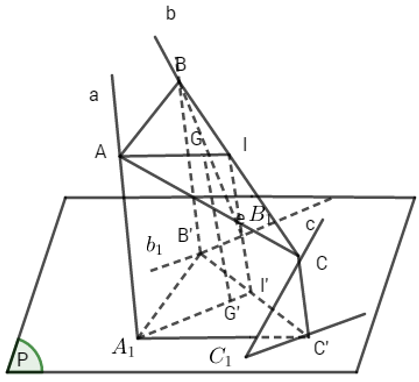
a) Phân tích
Giả sử dựng được tam giác ABC có ba đỉnh A, B, C lần lượt nằm trên ba đường thẳng a, b, c đôi một chéo nhau cho trước và nhận điểm G làm trọng tâm.
Lấy các điểm A1, B1, C1 lần lượt nằm trên a, b, c và gọi (P) là mp(A1B1C1). Xét phép chiếu song song lên mp(P) theo phương chiếu là đường thẳng a. Gọi tam giác A1B’C’ là hình chiếu của tam giác ABC. Khi đó trọng tâm G’ của tam giác A1B’C’ là hình chiếu của trọng tâm G của tam giác ABC, trung điểm I’ của B’C’ là hình chiếu của trung điểm I của BC.
Vậy khi đã chọn (P) thì các điểm A1,G’ dựng được và do đó I’ cũng dựng được. Ta chỉ cần dựng hai điểm B’ và C’ sao cho tam giác A1B’C’ nhận G’ làm trọng tâm với \(B' \in {b_1},C' \in {c_1}\) (b1, c1lần lượt là hình chiếu của b và c).
b) Cách dựng
Lấy ba điểm A1, B1, C1 tùy ý sao cho \({A_1} \in a,{B_1} \in b,{C_1} \in c\)
Xác định mặt phẳng (P) là mặt phẳng đi qua ba điểm A1, B1, C1.
Dựng các hình chiếu b1, c1 của b và c trên (P) theo phương chiếu a và dựng hình chiếu G’ của điểm G.
Trong mp(P), dựng điểm I’ sao cho \(\overrightarrow {{A_1}I'} = {3 \over 2}\overrightarrow {{A_1}G'} \)
Trong mp(P), dựng điểm \(B' \in {b_1},C' \in {c_1}\) sao cho I’ là trung điểm của B’C’.
Dựng điểm \(B \in b,C \in c\) sao cho BB’ // CC’ //a.
Dựng điểm \(I \in BC\) sao cho II’ // a, hay I là trung điểm của BC.
Trong mp(a, II’) dựng đường thẳng IG cắt a tại A.
Dựng tam giác ABC với ba điểm A, B, C vừa dựng được.
c) Chứng minh:
Vì AA1 // G'G // II'
Nên \({{AI} \over {AG}} = {{{A_1}I'} \over {{A_1}G'}} = {3 \over 2}\)
Suy ra G là trọng tâm tam giác ABC.
d) Biện luận. Bài toán có một nghiệm hình.

