Chứng minh rằng:
LG a
Hợp thành của hai phép đối xứng trục có các trục đối xứng song song là một phép tịnh tiến.
Lời giải chi tiết:
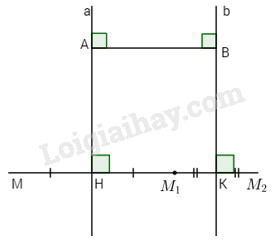
Giả sử Đa,Đb là các phép đối xứng trục có trục lần lượt là a, b mà a//b và F là hợp thành của Đa và Đb. Lấy hai điểm A, B lần lượt nằm trên a, b sao cho AB⊥a.
Với điểm M bất kì, Đa biến M thành M1 và Đb biến M1 thành M2.
Nếu gọi H và K lần lượt là trung điểm của MM1 và M1M2 thì:
→MM2=→MM1+→M1M2=2(→HM1+→M1K)=2→HK=2→AB
Vì phép hợp thành F biến M thành M2 thành →MM2=2→AB nên F là phép tịnh tiến theo vecto 2→AB.
LG b
Mỗi phép tịnh tiến đều có thể xem là hợp thành của hai phép đối xứng trục có trục đối xứng song song bằng nhiều cách.
Lời giải chi tiết:
Giả sử T là phép tịnh tiến theo vecto →u.
Lấy một đường thẳng a nào đó vuông góc với →u và đường thẳng b là ảnh của a qua phép tịnh tiến theo 12→u thì theo câu a) phép tịnh tiến T là hợp thành của phép đối xứng trục Đa và phép đối xứng trục Đb.
Vì có nhiều cách chọn đường thẳng a, nên có nhiều phép đối xứng Đa và Đb có hợp thành là T.
LG c
Hợp thành của một số chẵn các phép đối xứng trục có trục đối xứng song song là một phép tịnh tiến.
Lời giải chi tiết:
Hợp thành của hai phép đối xứng có trục đối xứng song song là một phép tịnh tiến.
Vì vậy, hợp thành của 2n phép đối xứng trục (có trục đối xứng song song) là hợp thành của n phép tịnh tiến
Do đó cũng là phép tịnh tiến.
LG d
Hơp thành của một số lẻ các phép đối xứng có trục đối xứng song song là một phép đối xứng trục.
Lời giải chi tiết:
Giả sử F là hợp thành của 2n + 1 phép đối xứng trục.
Gọi phép đối xứng trục thứ nhất là Đa (có trục là đường thẳng a), 2n phép đối xứng trục còn lại có hợp thành là phép tịnh tiến T.
Ta có thể xem T là hợp thành của hai phép đối xứng mà phép thứ nhất là Đa và phép thứ hai là Đb.
Vậy F là hợp thành của ba phép đối xứng: Đa, Đa và Đb.
Nhưng vì hợp thành của Đa và Đa là phép đồng nhất e nên F chính là phép đối xứng Đb.
LG e
Cho phép đối xứng trục Đa qua đường thẳng a và phép tịnh tiến T theo vecto →v vuông góc với a. Chứng tỏ rằng hợp thành của Đa và T là phép đối xứng trục, hợp thành của T và Đa cũng là phép đối xứng trục.
Lời giải chi tiết:
Có thể xem phép tịnh tiến T là hợp thành của hai phép đối xứng trục Đb và Đc.
Vì vecto tịnh tiến vuông góc với a nên a // b // c.
Do đó, ta được hợp thành của ba phép đối xứng có trục song song.
Vậy theo kết quả câu d) ta được một phép đối xứng trục.

