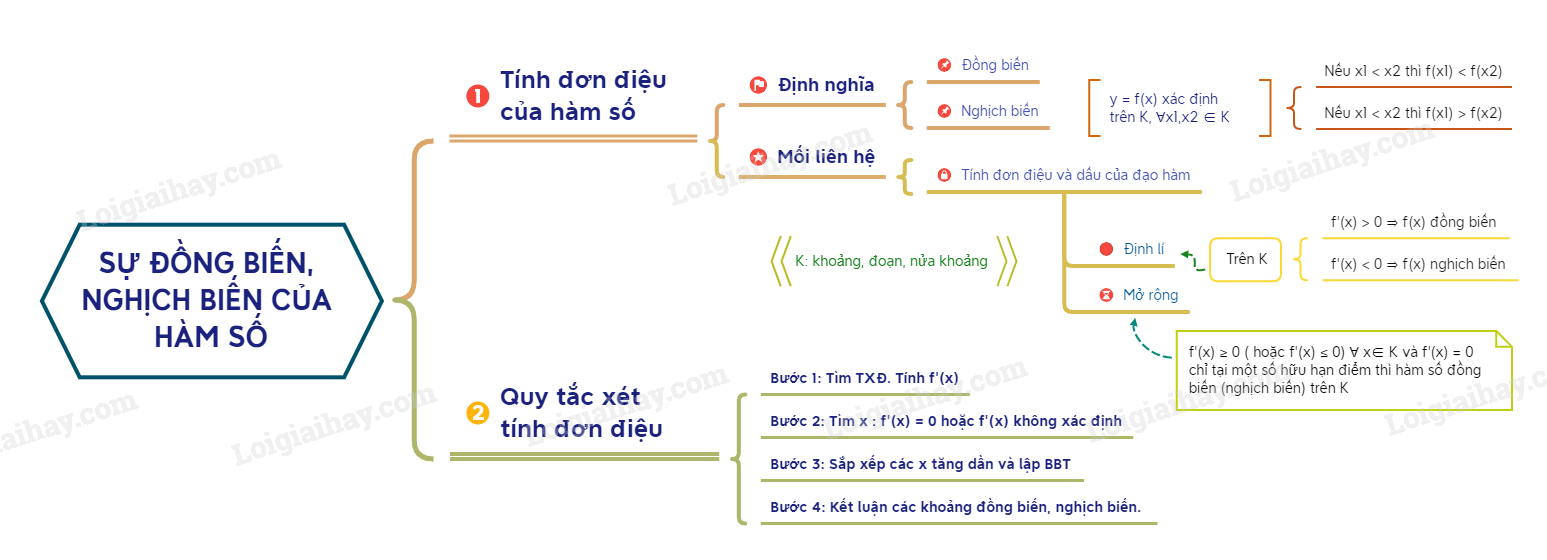
1. Định nghĩa
Hàm số \(f\) xác định trên \(K\). Với mọi \(x_1, x_2\) thuộc \(K\) mà \( x_1 > x_2\)
+) nếu \(f(x_1)>f(x_2)\) thì \(f\) tăng trên \(K\)
+) nếu \(f(x_1)<f(x_2)\) thì \(f\) giảm trên \(K\).
Chú ý:
- Hàm số tăng hoặc giảm trên \(K\) được gọi chung là hàm số đơn điệu trên \(K\).
- \(K\) có thể là một khoảng, một đoạn hoặc một nửa khoảng.
2. Điểu kiện cần đế hàm số đơn điệu
Cho hàm số \(f\) có đạo hàm trên khoảng \(K\)
- Nếu \(f\) tăng trên \(K\) thì \(f'(x)>0\), với mọi \(x\) thuộc \(K\).
- Nếu \(f\) giảm trên \(K\) thì \(f'(x)< 0\), với mọi \(x\) thuộc \(K\).
3. Điều kiện đủ để hàm số đơn điệu
Cho hàm sổ \(f\) có đạo hàm trên khoảng \(K\)
- Nếu \(f'(x) > 0\) với mọi \(x\) thuộc \(K\) thì \(f\) tăng trên \(K\).
- Nếu \(f'(x) < 0\) với mọi \(x\) thuộc \(K\) thì \(f\) giảim trên \(K\).
Chú ý: Nếu \(f'(x) ≥ 0\) \(\forall x \in K\) (hoặc \(f’(x) \le 0\), \(\forall x \in K\)) và \(f’(x) = 0\) chỉ tại một số hữu hạn điểm thuộc \(K\) thì hàm số \(f\) tăng (hoặc giảm) trên \(K\).