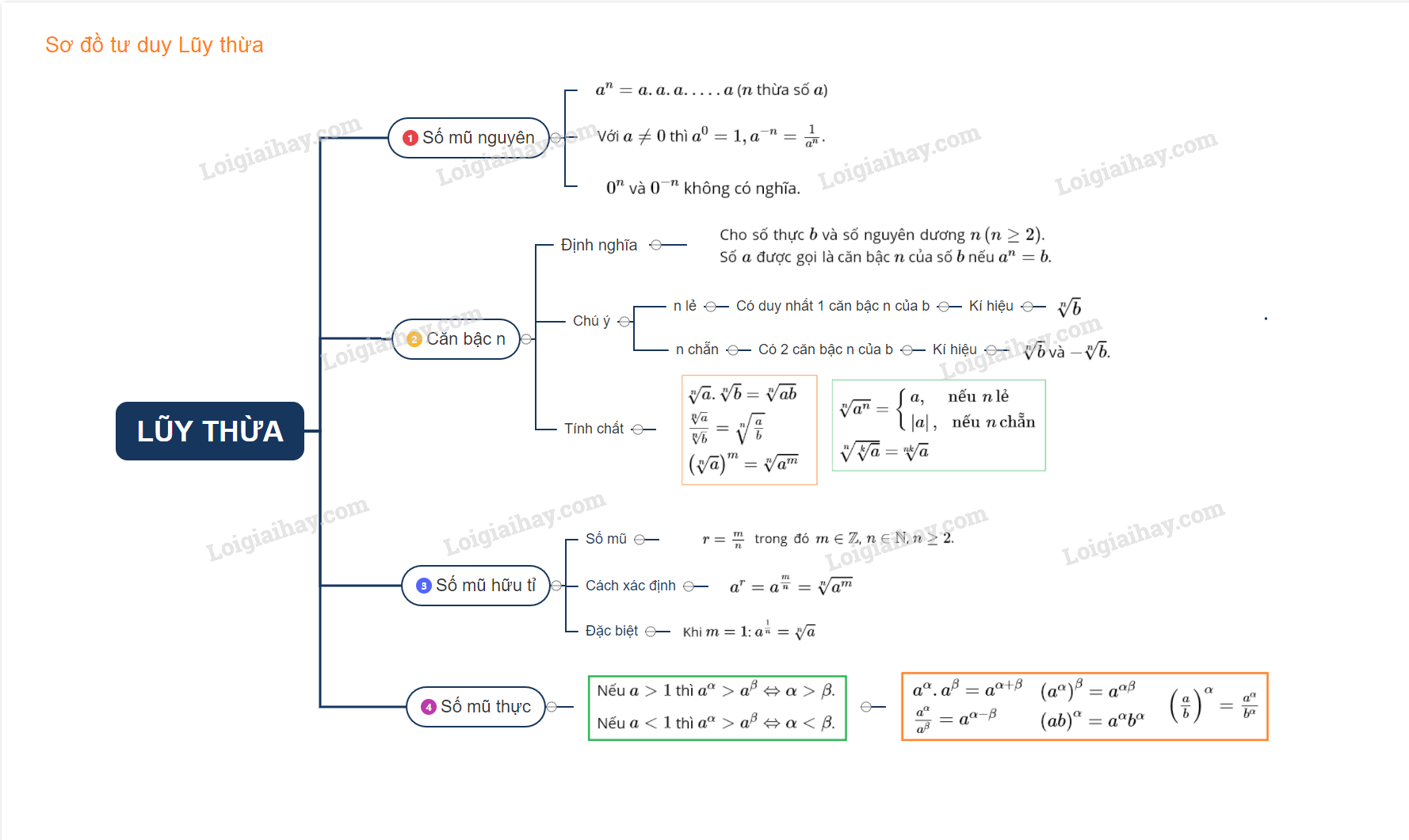
I. KHÁI NIỆM LŨY THỪA
1. Lũy thừa với số mũ nguyên
Định nghĩa
Cho \(n\) là một số nguyên dương.
Với \(a\) là một số thực tùy ý, lũy thừa bậc \(n\) của \(a\) là tích của \(n\) thừa số \(a\).
\({a^n} = a.a.a.....a\) (\(n\) thừa số \(a\))
Với \(a \ne 0\) thì \({a^0} = 1,{a^{ - n}} = \dfrac{1}{{{a^n}}}\).
Chú ý
\({0^n}\) và \({0^{ - n}}\) không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
2. Căn bậc \(n\)
a) Định nghĩa
Cho số thực \(b\) và số nguyên dương \(n\left( {n \ge 2} \right)\). Số \(a\) được gọi là căn bậc \(n\) của số \(b\) nếu \({a^n} = b\).
b) Chú ý
+) Với \(n\) lẻ và \(b \in \mathbb{R}\) thì có duy nhất một căn bậc \(n\) của \(b\), kí hiệu \(\sqrt[n]{b}\).
+) Với \(n\) chẵn và:
\(b < 0\) thì không tồn tại căn bậc \(n\) của \(b\).
\(b = 0\) thì có duy nhất một căn bậc \(n\) của \(b\) là số \(0\).
\(b > 0\) thì có hai căn trái dấu, kí hiệu \(\sqrt[n]{b}\) và \( - \sqrt[n]{b}\).
c) Tính chất
\(\begin{array}{l}\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\\\dfrac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\dfrac{a}{b}}}\\{\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\\\sqrt[n]{{{a^n}}} = \left\{ \begin{array}{l}a,\,\,\,\,\,\,\,\text{nếu} \,\,n \,\text{lẻ}\\\left| a \right|,\,\,\,\,\text{nếu}\,\,n\,\text{chẵn}\end{array} \right.\\\sqrt[n]{{\sqrt[k]{a}}} = \sqrt[{nk}]{a}\end{array}\)
Ví dụ
\(\sqrt[3]{{ - 4}}.\sqrt[3]{{54}} = \sqrt[3]{{\left( { - 4} \right).54}} = \sqrt[3]{{ - 216}} = - 6\)
3. Lũy thừa với số mũ hữu tỉ
Cho số thực \(a\) dương và số hữu tỉ \(r = \dfrac{m}{n}\), trong đó \(m \in \mathbb{Z}\), \(n \in \mathbb{N}\), \(n \ge 2\).
Lũy thừa của số \(a\) với số mũ \(r\) là số \({a^r}\) xác định bởi
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
Đặc biệt: Khi \(m=1\): \({a^{\frac{1}{n}}} = \sqrt[n]{a}\)
Ví dụ:
\({16^{ - \frac{3}{4}}} = \sqrt[4]{{{{16}^{ - 3}}}} = \dfrac{1}{{\sqrt[4]{{{{16}^3}}}}}\) \( = \dfrac{1}{{{{\left( {\sqrt[4]{{16}}} \right)}^3}}} = \dfrac{1}{{{2^3}}} = \dfrac{1}{8}\)
II. TÍNH CHẤT CỦA LŨY THỪA VỚI SỐ MŨ THỰC
Cho \(a,b\) là những số thực dương; \(\alpha ,\beta \) là những số thực tùy ý. Khi đó ta có:
\(\begin{array}{l}{a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\\\dfrac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }}\\{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }}\\{\left( {ab} \right)^\alpha } = {a^\alpha }{b^\alpha }\\{\left( {\dfrac{a}{b}} \right)^\alpha } = \dfrac{{{a^\alpha }}}{{{b^\alpha }}}\end{array}\)
Nếu \(a > 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \).
Nếu \(a < 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \).
Ví dụ: Rút gọn biểu thức: \(A = \dfrac{{{a^{\sqrt 2 + 1}}.{a^{3 - \sqrt 2 }}}}{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}\)
Ta có:
\(\begin{array}{l}
A = \dfrac{{{a^{\sqrt 2 + 1}}.{a^{3 - \sqrt 2 }}}}{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}} = \dfrac{{{a^{\sqrt 2 + 1 + 3 - \sqrt 2 }}}}{{{a^{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}}}\\
= \dfrac{{{a^4}}}{{{a^{3 - 1}}}} = {a^2}
\end{array}\)