Video hướng dẫn giải
Vẽ đồ thị của các hàm số:
LG a
a) \(y = \log x\);
Phương pháp giải:
Các bước khảo sát và vẽ đồ thị hàm số:
Bước 1: Tập xác định.
Bước 2: Sự biến thiên.
- Tính \(y'\), tìm các điểm mà tại đó \(y'\) bằng 0 hoặc không xác định.
- Xét dấu \(y'\) và suy ra các khoảng đơn điệu của đồ thị hàm số.
- Tính các giới hạn đặc biệt: Giới hạn tại vô cực và giới hạn tại các điểm mà hàm số không xác định.
- Tìm các tiệm cận của đồ thị hàm số (nếu có).
- Lập bảng biến thiên.
Bước 3: Đồ thị.
- Tìm giao điểm của đồ thị hàm số với các trục tọa độ (nếu có).
- Vẽ đồ thị hàm số dựa vào các yếu tố ở trên.
Lời giải chi tiết:
Đồ thị hàm số \(y = \log x\).
*) Tập xác định: \(D=(0;+\infty)\)
*) Sự biến thiên:
\(y' = {1 \over {x\ln 10}} > 0,\forall x \in D\)
- Hàm số đồng biến trên khoảng \((0;+\infty)\)
- Giới hạn đặc biệt:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = - \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)
Hàm số có tiệm cận đứng là: \(x=0\)
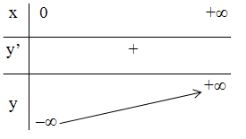
- Bảng biến thiên:
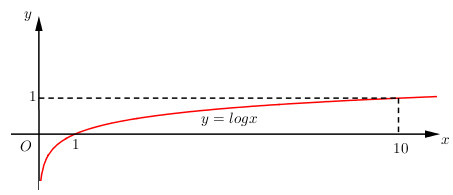
*) Đồ thị:
Đồ thị hàm số nằm hoàn toàn bên phải trục tung) nhận trục tung làm tiệm cận đứng, cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((10;1)\), \((\dfrac{1}{10}; -1)\).
LG b
b) y = \(\log_{\frac{1}{2}}x\).
Lời giải chi tiết:
Đồ thị hàm số \(y = \log_{\frac{1}{2}}x\).
*) Tập xác định: \(D=(0;+\infty)\)
*) Sự biến thiên:
\(y' = \dfrac {-1} {x\ln 2} < 0,\forall x \in D\)
- Hàm số nghịch biến trên khoảng \((0;+\infty)\)
- Giới hạn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr} \)
Hàm số có tiệm cận đứng \(x=0\).
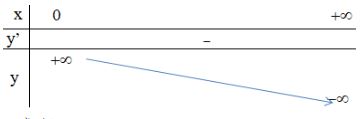
- Bảng biến thiên:
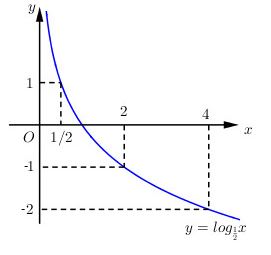
*) Đồ thị:
Đồ thị hàm số nằm hoàn toàn bên phải trục tung (nhận trục tung làm tiệm cận đứng), cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((\dfrac{1}{2};1)\), điểm phụ \((2;-1)\), \((4.-2)\), \((\dfrac{1}{4}; 2)\).