Đề bài
Câu 1. Tập nghiệm của bất phương trình \({\left( {{{\log }_2}x} \right)^2} - 4{\log _2}x + 3 > 0\) là:
A. \((0;2) \cup (8; + \infty )\).
B. \(( - \infty ;2) \cup (8; + \infty )\).
C. \((2;8)\)
D. \((8; + \infty )\).
Câu 2. Cho hàm số \(y = {2^x} - 2x\). Khẳng định nào sau đây sai :
A. Đồ thị hàm số luôn cắt trục tung.
B. Hàm số có giá trị nhỏ nhất lớn hơn -1.
C. Đồ thị hàm số cắt trục hoành tại duy nhất một điểm
D. Đồ thị hàm số luôn cắt đường thẳng y = 2
Câu 3. Nếu \({\log _a}x = {1 \over 2}{\log _a}9 - {\log _a}5 + {\log _a}2\,\,\,\,(a > 0,\,a \ne 1)\) thì x bằng:
A. \({2 \over 5}\) B. \({3 \over 5}\)
C. \({6 \over 5}\) D. \(3\).
Câu 4. Cho \(f(x) = \root 3 \of {{{x - 2} \over {x + 1}}} \). Đạo hàm f’(0) bằng:
A. 1 B. \({1 \over {\root 3 \of 4 }}\)
C. \(\root 3 \of 2 \) D. 4.
Câu 5. Đạo hàm của hàm số \(y = {\log _3}\left( {1 + \sqrt x } \right)\) là:
A. \(y' = {1 \over {(1 + \sqrt x )\ln 3}}\)
B. \(y' = {1 \over {\sqrt x (1 + \sqrt x )\ln 3}}\).
C. \(y' = {1 \over {2\sqrt x \ln 3}}\)
D. \(y' = {1 \over {2(\sqrt x + x)\ln 3}}\).
Câu 6. Cho x, y là hai số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây sai ?
A. \({x^m}.{x^n} = {x^{m + n}}\)
B. \({\left( {{x^n}} \right)^m} = {x^{nm}}\).
C. \({\left( {xy} \right)^n} = {x^n}.{y^n}\)
D. \({x^m}.{y^n} = {\left( {xy} \right)^{m + n}}\).
Câu 7. Tập nghiệm của bất phương trình \({\log _{{1 \over 2}}}(2x - 2) > {\log _{{1 \over 2}}}(x + 1)\) là:
A. \((2; + \infty )\) B. \(\left( {1;3} \right)\)
C. \(( - \infty ;3)\) D. \(\left( { - {1 \over 2};2} \right)\).
Câu 8. Nghiệm của phương trình \({\log _2}({\log _4}x) = 1\) là:
A. x = 16 B. x = 8
C. x = 4 D. x = 2.
Câu 9. Biết phương trình \({9^x} - {28.3^x} + 27 = 0\) có hai nghiệm x1 và x2. Tính tổng x1 + x2 ?
A. 0 B. 1
C. 2 D. 3
Câu 10. Cho biểu thức \({a^{{1 \over {\sqrt 3 }}}} > {a^{{1 \over {\sqrt 2 }}}}\,\,;\,\,\,{\log _b}{3 \over 4} < {\log _b}{4 \over 5}\) thì a và b thuộc:
A. 0 < a < 1, b > 1.
B. a > 1, b > 1.
C. 0 < a < 1, 0 < b < 1
D. a > 1, 0 < b <1.
Câu 11. Nghiệm của bất phương trình \({\log _2}({3^x} - 2) < 0\) là:
A. x < 1 B. \({\log _3}2 < x < 1\)
C. 0 < x < 1 D. x > 1.
Câu 12. Cho hàm số \(y = {e^x}(\sin x - \cos x)\). Ta có y’ bằng:
A. \(2{e^x}\sin x\) B. \( - 2{e^x}\sin x\) C. \( - 2{e^x}\cos x\) D. \(2{e^x}\cos x\)
Câu 13. Biểu thức \(\left( {\root 3 \of a + \root 3 \of b } \right)\left( {{a^{{2 \over 3}}} + {b^{{2 \over 3}}} - \root 3 \of {ab} } \right)\) có giá trị ( với a, b dương) là:
A. \({a^{{2 \over 3}}} + {b^{{2 \over 3}}}\)
B. a – b
C. a + b
D. \({a^{{3 \over 2}}} + {b^{{3 \over 2}}}\).
Câu 14. Gọi x1, x2 là hai nghiệm của phương trình \({\log _3}^2x - 3{\log _3}x + 2 = 0\). Giá trị biểu thức \(P = {x_1}^2 + {x_2}^2\) bằng bao nhiêu ?
A. 20 B. 92
C. 90 D. 9
Câu 15. Rút gọn biểu thức \(P = {a^{{5 \over 3}}}:\sqrt a \,\,\,\,\,(a > 0)\) .
A. \(P = {a^{{2 \over 3}}}\)
B. \(P = {a^{{{ - 2} \over 3}}}\)
C. \(P = {a^{{4 \over 3}}}\)
D. \(P = {a^{{7 \over 6}}}\)
Câu 16. Tập nghiệm của bất phương trình \({3^x} \ge 5 - 2x\) là:
A. \([1; + \infty )\) B. \(\emptyset \)
C. \((1; + \infty )\) D. \(( - \infty ;1]\).
Câu 17. Cho \(a > 0,\,n \in Z,n \ge 2\), chọn khẳng định đúng:
A. \({a^{{1 \over n}}} = \root n \of a \)
B. \({a^{{1 \over n}}} = \sqrt {{a^n}} \)
C. \({a^{{1 \over n}}} = {a^n}\)
D. \({a^{{1 \over n}}} = \root a \of n \)
Câu 18. Chọn mệnh đề đúng :
A. \({\log _a}1 = 1\)
B. \({\log _a}a = a\)
C. \({\log _a}1 = a\)
D. \({\log _a}a = 1\)
Câu 19. Với các số thực a, b > 0 bất kì. Rút gọn biểu thức \(P = 2{\log _2}a - {\log _{{1 \over 2}}}{b^2}\):
A. \(P = {\log _2}{\left( {{a \over b}} \right)^2}\)
B. \(P = {\log _2}\left( {{{2a} \over {{b^2}}}} \right)\).
C. \(P = {\log _2}(2a{b^2})\)
D. \(P = {\log _2}{(ab)^2}\).
Câu 20. Cho các số thực a < b < 0. Mệnh đề nào sau đây sai ?
A. \(\ln {(ab)^2} = \ln ({a^2}) + \ln ({b^2})\).
B. \(\ln \left( {\sqrt {ab} } \right) = {1 \over 2}\left( {\ln a + \ln b} \right)\)
C. \(\ln \left( {{a \over b}} \right) = \ln |a| - \ln |b|\).
D. \(\ln {\left( {{a \over b}} \right)^2} = \ln ({a^2}) - \ln ({b^2})\).
Câu 21. Bất phương trình \({\log _{{1 \over 3}}}{{3x - 1} \over {x + 2}} < 1\) có nghiệm là:
A. \(x = {3 \over 4}\)
B. \(x = 4\)
C. \(x \in ( - \infty ; - 2) \cup \left( {{5 \over 8}; + \infty } \right)\)
D. \(x \in ( - 9;2) \cup (8; + \infty )\).
Câu 22. Biểu thức \({a^3} + {a^{ - 3}}\) bằng:
A. \(\left( {a - {1 \over a}} \right)\left( {{a^2} - 2 + {1 \over {{a^2}}}} \right)\). B. \(\left( {a + {1 \over a}} \right)\left( {{a^2} - 1 + {1 \over {{a^2}}}} \right)\).
C. \(\left( {{1 \over a} - a} \right)\left( {{a^2} + 1 + {1 \over {{a^2}}}} \right)\) D. \(\left( {a - {1 \over a}} \right)\left( {{a^2} + 1 + {1 \over {{a^2}}}} \right)\).
Câu 23. Biết \(3 + 2{\log _2}x = {\log _2}y\(. Hãy biểu thị y theo x.
A. \(y = 2x + 3\)
B. \(y = 8{x^2}\).
C. \(y = {x^2} + 8\)
D. \(y = 3{x^2}\).
Câu 24. Với \(0 < x \ne 1\) , biểu thức \({1 \over {{{\log }_3}x}} + {1 \over {{{\log }_4}x}} + {1 \over {{{\log }_5}x}}\) bằng
A. \({1 \over {{{\log }_x}60}}\)
B. \({1 \over {({{\log }_3}x)({{\log }_4}x)({{\log }_5}x)}}\).
C. \({1 \over {{{\log }_{60}}x}}\)
D. \({1 \over {{{\log }_3}x + {{\log }_4}x + {{\log }_5}x}}\).
Câu 25. Tìm miền xác định của hàm số \(y = \log \left( {{{1 - 5x} \over {2 - x}}} \right)\).
A. \(D = \left( { - \infty ;{1 \over 5}} \right) \cup \left( {2; + \infty } \right)\).
B. \(D = \left( { - \infty ;2} \right) \cup \left( {{1 \over 5}; + \infty } \right)\).
C. \(D = ( - \infty ;2] \cup \left[ {{1 \over 5}; + \infty } \right)\)
D. \(\left( { - \infty ;{1 \over 5}} \right) \cap \left( {2; + \infty } \right)\).
Phương pháp giải - Xem chi tiết
Lời giải chi tiết
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | A | C | C | B | D |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | D | B | A | D | A |
| Câu | 11 | 12 | 13 | 14 | 15 |
| Đáp án | B | A | C | C | D |
| Câu | 16 | 17 | 18 | 19 | 20 |
| Đáp án | A | A | D | D | B |
| Câu | 21 | 22 | 23 | 24 | 25 |
| Đáp án | C | B | B | A | A |
Câu 1.
Điều kiện: \(x > 0\)
Ta có: \({\left( {{{\log }_2}x} \right)^2} - 4{\log _2}x + 3 > 0 \)
\(\Leftrightarrow \left( {{{\log }_2}x - 1} \right)\left( {{{\log }_2}x - 3} \right) > 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{\log _2}x - 1 > 0\\{\log _2}x - 3 > 0\end{array} \right.\\\left\{ \begin{array}{l}{\log _2}x - 1 < 0\\{\log _2}x - 3 < 0\end{array} \right.\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 2\\x > 8\end{array} \right.\\\left\{ \begin{array}{l}x < 2\\x < 8\end{array} \right.\end{array} \right. \)
\(\Leftrightarrow x \in \left( { - \infty ;2} \right) \cup \left( {8; + \infty } \right)\)
Chọn đáp án B.
Câu 2.
Phương trình hoành độ giao điểm của hàm số vói trục hoành là:
\({2^x} - 2x = 0 \Leftrightarrow {2^x} = 2x \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
Khẳng định C sai.
Chọn đáp án C.
Câu 3.
Ta có: \({\log _a}x = \dfrac{1}{2}{\log _a}9 - {\log _a}5 + {\log _a}2\, \)\(= {\log _a}3 - {\log _a}5 + {\log _a}2\)
\( \Leftrightarrow {\log _a}x = {\log _a}6 - {\log _a}5 = {\log _a}\dfrac{6}{5} \)
\(\Leftrightarrow x = \dfrac{6}{5}.\)
Chọn đáp án C.
Câu 4.
Ta có: \(f(x) = \sqrt[3]{{\dfrac{{x - 2}}{{x + 1}}}}\)
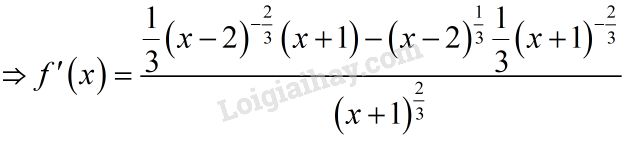
Khi đó \(f'\left( 0 \right) = \dfrac{1}{{\sqrt[4]{3}}}\).
Câu 5.
Ta có:
\(\begin{array}{l}y' = [{\log _3}\left( {1 + \sqrt x } \right)]'\\\;\;\; = \dfrac{{{{\left( {1 + \sqrt x } \right)}^\prime }}}{{\left( {1 + \sqrt x } \right)\ln 3}}\\\;\;\; = \dfrac{1}{{2\sqrt x \left( {1 + \sqrt x } \right)\ln 3}} \\\;\;\;= \dfrac{1}{{2\left( {x + \sqrt x } \right)\ln 3}}\\\end{array}\)
Chọn đáp án D.
Câu 6.
Đẳng thức sai là \({x^m}.{y^n} = {\left( {xy} \right)^{m + n}}\)
Chọn đáp án D.
Câu 7.
Điều kiện: \(x > 1.\)
Ta có: \({\log _{\dfrac{1}{2}}}(2x - 2) > {\log _{\dfrac{1}{2}}}(x + 1)\)
\(\Leftrightarrow 2x - 2 < x + 1\)
\( \Leftrightarrow x < 3\)
Kết hợp điều kiện: \(x \in \left( {1;3} \right)\)
Chọn đáp án B.
Câu 8.
Điều kiện: \(\left\{ \begin{array}{l}{\log _4}x > 0\\x > 0\end{array} \right. \Leftrightarrow x > 1\)
Ta có: \({\log _2}({\log _4}x) = 1 \Leftrightarrow {\log _4}x = 2 \)
\(\Leftrightarrow x = {4^2} = 16.\)
Chọn đáp án A.
Câu 9.
Ta có: \({9^x} - {28.3^x} + 27 = 0\)
\(\Leftrightarrow {\left( {{3^x}} \right)^2} - 28\left( {{3^x}} \right) + 27 = 0\)
\( \Leftrightarrow \left( {{3^x} - 1} \right)\left( {{3^x} - 27} \right) = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}{3^x} = 1\\{3^x} = 27\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\)
Khi đó \({x_1} + {x_2} = 3.\)
Chọn đáp án D.
Câu 10.
Ta có: \({a^{\dfrac{1}{{\sqrt 3 }}}} > {a^{\dfrac{1}{{\sqrt 2 }}}}\,\,;\)
\({\log _b}\dfrac{3}{4} < {\log _b}\dfrac{4}{5}\)
\(\Rightarrow \left\{ \begin{array}{l}0 < a < 1\\b > 1\end{array} \right.\)
Chọn đáp án A.
Câu 11.
Điều kiện: \({3^x} > 2\)\( \Leftrightarrow x > {\log _3}2\)
Ta có: \({\log _2}({3^x} - 2) < 0\)
\(\Leftrightarrow {3^x} - 2 < 1 \)
\(\Leftrightarrow {3^x} < 3 \)
\(\Leftrightarrow x < 1.\)
Chọn đáp án B.
Câu 12.
Ta có: \(y = {e^x}(\sin x - \cos x) \)
\(\Rightarrow y' = {e^x}(\sin x - \cos x) + {e^x}\left( {\cos x + \sin x} \right) \)\(\,= 2{e^x}\sin x\)
Chọn đáp án A.
Câu 13.
Ta có: \(\left( {\sqrt[3]{a} + \sqrt[3]{b}} \right)\left( {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}} - \sqrt[3]{{ab}}} \right) \)
\(\,= \left( {{a^{\dfrac{1}{3}}} + {b^{\dfrac{1}{3}}}} \right)\left( {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}} - {a^{\dfrac{1}{3}}}{b^{\dfrac{1}{3}}}} \right) \)
\(= a + b\)
Chọn đáp án C.
Câu 14.
Điều kiện: \(x > 0\)
Ta có: \({\log _3}^2x - 3{\log _3}x + 2 = 0\)
\(\Leftrightarrow \left( {{{\log }_3}x - 1} \right)\left( {{{\log }_3}x - 2} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = 2\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 9\end{array} \right.\)
Khi đó ta có: \(P = {x_1}^2 + {x_2}^2 = {3^2} + {9^2} = 90.\)
Chọn đáp án C.
Câu 15.
Ta có: \(P = {a^{\dfrac{5}{3}}}:\sqrt a \,\, = {a^{\dfrac{5}{3}}}:{a^{\dfrac{1}{2}}} \)\(\,= {a^{\dfrac{5}{3} - \dfrac{1}{2}}} = {a^{\dfrac{7}{6}}}\)
Chọn đáp án D.
Câu 16.
Xét hàm số: \(y = {3^x} + 2x - 5\)\(\, \Rightarrow y' = {3^x}\ln 3 + 2 > 0\)
\( \to \) Hàm số đồng biến trên tập xác định.
Khi đó ta có: \(y\left( 1 \right) = 0\)\( \Rightarrow \) Bất phương trình đã cho có tập nghiệm là \([1; + \infty )\)
Chọn đáp án A.
Câu 17.
Với \(a > 0,\,n \in Z,n \ge 2\) ta có \({a^{\dfrac{1}{n}}} = \sqrt[n]{a}\)
Chọn đáp án A.
Câu 18.
Ta có: \({\log _a}a = 1\) là mệnh đề đúng.
Chọn đáp án D.
Câu 19.
Ta có: \(P = 2{\log _2}a - {\log _{\dfrac{1}{2}}}{b^2} \)
\(= 2{\log _2}a + {\log _2}b{}^2 = 2{\log _2}a + 2{\log _2}b\)
\(= 2{\log _2}\left( {ab} \right) = {\log _2}{\left( {ab} \right)^2}\)
Chọn đáp án D.
Câu 20.
Điều kiện của hàm logarit là \(a,b > 0\)
Khi đó ta có: \(\ln \left( {\sqrt {ab} } \right) = \dfrac{1}{2}\left( {\ln a + \ln b} \right)\) là mệnh đề sai.
Chọn đáp án B.
Câu 21.
Điều kiện: \(\dfrac{{3x - 1}}{{x + 2}} > 0\)
\(\Leftrightarrow x \in \left( { - \infty ; - 2} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right)\)
Khi đó ta có: \({\log _{\dfrac{1}{3}}}\dfrac{{3x - 1}}{{x + 2}} < 1\)
\(\Leftrightarrow \dfrac{{3x - 1}}{{x + 2}} > \dfrac{1}{3} \)
\(\Leftrightarrow \dfrac{{8x - 5}}{{3\left( {x + 2} \right)}} > 0\)
\( \Leftrightarrow x \in \left( { - \infty ; - 2} \right) \cup \left( {\dfrac{5}{8}; + \infty } \right)\)
Khết hợp điều kiện: \(x \in ( - \infty ; - 2) \cup \left( {\dfrac{5}{8}; + \infty } \right)\)
Chọn đáp án C.
Câu 22.
Ta có: \({a^3} + {a^{ - 3}} = {a^3} + \dfrac{1}{{{a^3}}} \)\(\,= \left( {a + \dfrac{1}{a}} \right)\left( {{a^2} + \dfrac{1}{{{a^2}}} - 1} \right)\)
Chọn đáp án B.
Câu 23.
Ta có: \(3 + 2{\log _2}x = {\log _2}y\)
\(\Leftrightarrow {\log _2}y = {\log _2}{x^2} + {\log _2}{2^3} = {\log _2}\left( {8{x^2}} \right)\)
Khi đó ta có: \(y = 8{x^2}\)
Chọn đáp án B.
Câu 24.
Ta có: \(\dfrac{1}{{{{\log }_3}x}} + \dfrac{1}{{{{\log }_4}x}} + \dfrac{1}{{{{\log }_5}x}}\)
\(= {\log _x}3 + {\log _x}4 + {\log _x}5 = {\log _x}\left( {3.4.5} \right) \)
\(= {\log _x}60 = \dfrac{1}{{{{\log }_{60}}x}}\)
Chọn đáp án C.
Câu 25.
Điều kiện xác định: \(\dfrac{{1 - 5x}}{{2 - x}} > 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}1 - 5x > 0\\2 - x > 0\end{array} \right.\\\left\{ \begin{array}{l}1 - 5x < 0\\2 - x < 0\end{array} \right.\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < \dfrac{1}{5}\\x < 2\end{array} \right.\\\left\{ \begin{array}{l}x > \dfrac{1}{5}\\x > 2\end{array} \right.\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x < \dfrac{1}{5}\\x > 2\end{array} \right.\)
Chọn đáp án A.

