Đề bài
Cho hình lập phương \((H)\). Gọi \((H’)\) là hình bát diện đều có các đỉnh là tâm các mặt của \((H)\). Tính tỉ số diện tích toàn phần của \((H)\) và \((H’)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Bát diện đều là khối đa diện gồm 8 mặt là 8 tam giác đều.
+) Diện tích toàn phần của hình bát diện đều = 8. diện tích 1 mặt.
Lời giải chi tiết
Giả sử khối lập phương có cạnh bằng \(a\). Khi đó diện tích toàn phần của nó là: \(S_1 = 6a^2\)
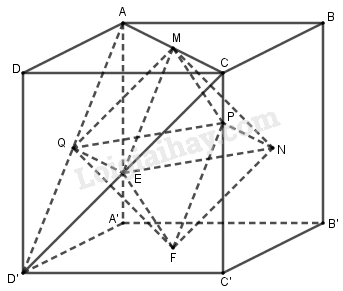
Gọi \(M\) là tâm của hình vuông \(ABCD\); \(Q\) là tâm hình vuông \(ADD'A'\); \(P\) là tâm hình vuông \(ABB'A'\); \(N\) là tâm hình vuông \(BCC'B'\); \(E\) là tâm hình vuông \(DCC'D'\) và \(F\) là tâm hình vuông \(A'B'C'D'\).
Xét bát diện đều thu được, khi đó diện tích toàn phần của nó là \(8\) lần diện tích tam giác đều \(MQE\) (hình vẽ)
Xét tam giác \(ACD’\), ta có \(M, Q\) lần lượt là trung điểm của \(AC\) và \(AD’\) nên \(MQ\) là đường trung bình của tam giác \(ACD’\), do đó \(MQ = \displaystyle{1 \over 2}C{\rm{D}}' = \displaystyle{{a\sqrt 2} \over 2} \)
Ta có \({S_{MQE}} = \displaystyle{1 \over 2}{\left( {\displaystyle{{a\sqrt 2} \over 2} } \right)^2}.{{\sqrt 3 } \over 2} = {{\sqrt 3 {a^2}} \over 8} \)
Diện tích xung quanh của bát diện đều là: \({S_2} = 8.\displaystyle{{\sqrt 3 {a^2}} \over 8} = {a^2}\sqrt 3 \)
Do đó: \(\displaystyle{{{S_1}} \over {{S_2}}} = {{6{{\rm{a}}^2}} \over {a^2\sqrt 3 }} = 2\sqrt 3 \)