Phần 1
Nguyên hàm
Câu 1. Cho \(y = f\left( x \right),y = g\left( x \right)\)là các hàm số liên tục trên \(\mathbb{R}\). Tìm khẳng định sai trong các khẳng định sau:
A. \(\int {k.f\left( x \right)dx} = k.\int {f\left( x \right)dx} \) với \(k \in \mathbb{R}\backslash \left\{ 0 \right\}\)
B. \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} + \int {g\left( x \right)dx} \)
C. \(\int {\left[ {f\left( x \right).g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} .\int {g\left( x \right)dx} \)
D. \(\left[ {\int {f\left( x \right)dx} } \right]' = f\left( x \right)\).
Câu 2. \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = x.{e^{{x^2}}}\). Hàm số nào sau đây không phải là \(F\left( x \right)\)?
A. \(F\left( x \right) = \frac{1}{2}{e^{{x^2}}} + 2\)
B. \(F\left( x \right) = \frac{1}{2}\left( {{e^{{x^2}}} + 5} \right)\)
C. \(F\left( x \right) = - \frac{1}{2}{e^{{x^2}}} + C\)
D. \(F\left( x \right) = - \frac{1}{2}\left( {2 - {e^{{x^2}}}} \right)\)
Câu 3. Cho hai hàm số \(F\left( x \right) = \left( {{x^2} + ax + b} \right).{e^{ - x}}\) và \(f\left( x \right) = \left( { - {x^2} + 3x + 6} \right).{e^{ - x}}\). Tìm a và b để \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\).
A. a = 1, b = -7
B. a = - 1, b = - 7
C. a = - 1 , b = 7
D. a = 1, b = 7.
Câu 4. \(F\left( x \right) = \left( {a{x^3} + b{x^2} + cx + d} \right).{e^{ - x}} + 2018e\) là một nguyên hàm của hàm số \(f\left( x \right) = \left( { - 2{x^3} + 3{x^2} + 7x - 2} \right){e^{ - x}}\). Khi đó:
A. \(a + b + c + d = 4\)
B. \(a + b + c + d = 5\)
C. \(a + b + c + d = 6\)
D. \(a + b + c + d = 7\)
Câu 5. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{3}{{{x^2}}}\) là:
A. \(\int {f\left( x \right)dx} = 3\ln {x^2} + C\)
B. \(\int {f\left( x \right)dx} = - \frac{3}{x} + C\)
C. \(\int {f\left( x \right)dx} = \frac{3}{{{x^2}}} + C\)
D. \(\int {f\left( x \right)dx} = \frac{3}{x} + C\)
Câu 6. Hàm số \(F\left( x \right) = \tan x + 2\) là một nguyên hàm của hàm số nào dưới đây?
A. \(f\left( x \right) = - \frac{1}{{{{\sin }^2}x}}\)
B. \(f\left( x \right) = \frac{1}{{{{\sin }^2}x}}\)
C. \(f\left( x \right) = \frac{1}{{{{\cos }^2}x}}\)
D. \(f\left( x \right) = - \frac{1}{{{{\cos }^2}x}}\)
Câu 7. Tìm \(\int {\left( {1 - x} \right)\cos xdx} \)
A. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 - x} \right)\sin x - \cos x + C\)
B. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 + x} \right)\sin x - \cos x + C\)
C. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 - x} \right)\sin x + \cos x + C\)
D. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 - x} \right)\sin x - \sin x + C\)
Câu 8. Biết \(\int {f\left( x \right)dx} = 2x\ln \left( {3x - 1} \right) + C\). Tìm khẳng định đúng trong các khẳng định sau:
A. \(\int {f\left( {3x} \right)dx} = 6x\ln \left( {3x - 1} \right) + C\)
B. \(\int {f\left( {3x} \right)dx} = 6x\ln \left( {3x - 1} \right) + C\)
C. \(\int {f\left( {3x} \right)dx} = 3x\ln \left( {9x - 1} \right) + C\)
D. \(\int {f\left( {3x} \right)dx} = 2x\ln \left( {9x - 1} \right) + C\)
Câu 9. Tìm nguyên hàm \(\int {\frac{{2{x^3} - 6{x^2} + 4x + 1}}{{{x^2} - 3x + 2}}} dx\)
A. \({x^2} + \ln \left| {\frac{{x - 1}}{{x - 2}}} \right| + C\)
B. \(\frac{1}{2}{x^2} + \ln \left| {\frac{{x - 2}}{{x - 1}}} \right| + C\)
C. \(\frac{1}{2}{x^2} + \ln \left| {\frac{{x - 1}}{{x - 2}}} \right| + C\)
D. \({x^2} + \ln \left| {\frac{{x - 2}}{{x - 1}}} \right| + C\)
Câu 10. Tìm nguyên hàm \(\int {\frac{{2x - 1}}{{{{\left( {x + 1} \right)}^2}}}dx} \)
A. \(2\ln \left| {x + 1} \right| - \frac{3}{{x + 1}} + C\)
B. \(2\ln \left| {x + 1} \right| + \frac{3}{{x + 1}} + C\)
C. \( - \ln \left| {x + 1} \right| + \frac{3}{{x + 1}} + C\)
D. \(\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C\).
Câu 11. Tính \(\int {\frac{{dx}}{{\sqrt {1 - x} }}} \) thu được kết quả là:
A. \(\frac{C}{{\sqrt {1 - x} }}\)
B. \( - 2\sqrt {1 - x} + C\)
C. \(\frac{2}{{\sqrt {1 - x} }} + C\)
D. \(\sqrt {1 - x} + C\)
Câu 12. Cho \(\int {\frac{{dx}}{{\sqrt {x + 2} + \sqrt {x + 1} }} = a\left( {x + 2} \right)\sqrt {x + 2} + b\left( {x + 1} \right)\sqrt {x + 1} + C} \). Khi đó 3a+b bằng:
A. \( - \frac{2}{3}\) B. \(\frac{1}{3}\)
C. \(\frac{4}{3}\) D. \(\frac{2}{3}\)
Câu 13. Họ nguyên hàm của hàm số \(f\left( x \right) = {\cos ^2}2x\) là:
A. \(\frac{1}{2} + \frac{{\sin 4x}}{8} + C\)
B. \(\frac{x}{2} - \frac{{\sin 4x}}{2} + C\)
C. \(\frac{1}{2} - \frac{{\sin 4x}}{2} + C\)
D. \(\frac{x}{2} + \frac{{\sin 4x}}{8} + C\)
Câu 14. Họ nguyên hàm của hàm số \(f\left( x \right) = {\tan ^2}x\) là:
A. \(\cot x - x + C\)
B. \(\tan x - x + C\)
C. \( - \cot x - x + C\)
D. \( - \tan x - x + C\).
Câu 15. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{\sin x}}\) là:
A. \(\ln \left| {\cot \frac{x}{2}} \right| + C\)
B. \(\ln \left| {\tan \frac{x}{2}} \right| + C\)
C. \( - \ln \left| {\tan \frac{x}{2}} \right| + C\)
D. \(\ln \left| {\sin x} \right| + C\).
Câu 16. Họ nguyên hàm của hàm số \(f\left( x \right) = 2x.{x^{{x^2}}}\) là:
A. \(\frac{1}{{{2^{{x^2}}}\ln 2}} + C\)
B. \(\frac{1}{{\ln 2}}{2^{{x^2}}} + C\)
C. \(\frac{{\ln 2}}{{{2^{{x^2}}}}} + C\)
D. \({2^{{x^2}}}\ln 2 + C\).
Câu 17. Tìm \(\int {{e^{{{\sin }^2}x}}\sin 2xdx} \)?
A. \({e^{{{\sin }^2}x}} + C\)
B. \(\sin x{e^{\tan x}} + C\)
C. \({e^{\tan x}} + C\)
D. \({e^{\sin 2x}} + C\)
Câu 18. Họ nguyên hàm của hàm số \(f\left( x \right) = x.\sqrt[3]{{3x - 1}}\) là:
A. \(\frac{1}{{21}}\sqrt[3]{{{{\left( {3x - 1} \right)}^7}}} + \frac{1}{{15}}\sqrt[3]{{{{\left( {3x - 1} \right)}^5}}} + C\)
B. \(\frac{1}{{18}}\sqrt[3]{{{{\left( {3x - 1} \right)}^6}}} + \frac{1}{{12}}\sqrt[3]{{{{\left( {3x - 1} \right)}^4}}} + C\)
C. \(\frac{1}{9}\sqrt[3]{{{{\left( {3x - 1} \right)}^3}}} + \sqrt[3]{{3x - 1}} + C\)
D. \(\frac{1}{{12}}\sqrt[3]{{{{\left( {3x - 1} \right)}^4}}} + \frac{1}{3}\sqrt[3]{{3x - 1}} + C\)
Câu 19. Tìm \(T = \int {\frac{{dx}}{{\cos x.{{\sin }^3}x}}} \)
A. \( - \ln \left| {\cot x} \right| - \frac{1}{2}{\cot ^2}x + C\)
B. \( - \ln \left| {\sin x} \right| - \frac{1}{2}\cot x + C\)
C. \( - \ln \left| {\cot x} \right| + {\cot ^2}x + C\)
D. \( - \ln \left| {\tan x} \right| - \frac{1}{2}{\cot ^2}x + C\)
Câu 20. Họ nguyên hàm của hàm số \(f\left( x \right) = {x^2}.{e^{{x^3} + 1}}\) là:
A. \(\arcsin \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{4} + C\)
B. \(2\arccos \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{2} + C\)
C. \(\arccos \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{4} + C\)
D. \(2\arcsin \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{2} + C\)
Phần 2
Tích phân
Câu 1. Cho \(\int\limits_0^2 {f\left( x \right)dx} = - 1,\int\limits_0^2 {g\left( x \right)dx} = 1\). Khi đó \(\int\limits_0^2 {\left[ {f\left( x \right) + g\left( x \right) + 1} \right]dx} \) bằng:
A. 1 B. 4 C. 2 D. 0
Câu 2. Biết rằng \(\int\limits_0^{\frac{\pi }{4}} {x\cos 2xdx} = \frac{\pi }{a} + \frac{1}{b}\), với \(a,b \in \mathbb{Z}\). Khẳng định nào sau đây đúng?
A. \(a + b = 4\)
B. \(a + b = 3\)
C. \(a + b = - 1\)
D. \(a + b = 1\)
Câu 3. Biết \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right) = 4{x^3} - \frac{1}{{{x^2} + 3x}}\) và thỏa mãn \(F\left( 1 \right) + 2F\left( 2 \right) = 2\). Tính \(F\left( 2 \right)\)
A. \(F\left( 2 \right) = 38\)
B. \(F\left( 2 \right) = \frac{{86}}{7}\)
C. \(F\left( 2 \right) = 7\)
D. \(F\left( 2 \right) = \frac{{151}}{4}\)
Câu 4. Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( {3x} \right) = 2f\left( x \right)\), với \(\forall x \in \mathbb{R}\). Biết rằng \(\int\limits_0^2 {f\left( x \right)dx} = 2\). Giá trị của tích phân \(\int\limits_0^6 {f\left( x \right)dx} \) bằng:
A. 4 B. 2 C. 6 D. 12
Câu 5. Cho hàm số \(f\left( x \right)\) có đạo hàm tại \(\forall x \in \mathbb{R}\) và \(f\left( x \right) > 0,\forall x \in \mathbb{R}\). Biết \(f'\left( x \right) = f\left( x \right).{e^x}\) và \(f\left( 1 \right) = e\). Tính \(J = \int\limits_0^2 {\ln \left[ {f\left( x \right)} \right]dx} \).
A. \(J = {e^2} - 2e + 1\)
B. \(J = {e^2} - 2e - 1\)
C. \(J = {e^2} - e + 1\)
D. \(J = {e^4} - 2e - 1\)
Câu 6. Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) thỏa \(f'\left( x \right) = \frac{1}{{x - 1}};f\left( 0 \right) = 1;f\left( 2 \right) = 2\). Tính \(f\left( { - 3} \right) + f\left( 3 \right)\).
A. \(2 + 3\ln 2\)
B. \(1 + 3\ln 2\)
C. \(3 + 3\ln 2\)
D. \(4 + 3\ln 2\)
Câu 7. Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Khi đó hiệu số \(F\left( - \right) - F\left( 1 \right)\) bằng:
A. \(\int\limits_0^1 {f\left( x \right)dx} \)
B. \(\int\limits_0^1 { - F\left( x \right)dx} \)
C. \(\int\limits_0^1 {F\left( x \right)dx} \)
D. \(\int\limits_0^1 { - f\left( x \right)dx} \)
Câu 8. Tính tích phân \(I = \int\limits_0^1 {{x^{2018}}\left( {1 + x} \right)dx} \)
A. \(I = \frac{1}{{2018}} + \frac{1}{{2019}}\)
B. \(I = \frac{1}{{2020}} + \frac{1}{{2021}}\)
C. \(I = \frac{1}{{2019}} + \frac{1}{{2020}}\)
D. \(I = \frac{1}{{2017}} + \frac{1}{{2018}}\)
Câu 9. Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\frac{2}{{x + 1}}{\rm{ khi }}0 \le x \le 1\\2x - 1{\rm{ khi 1}} \le {\rm{x}} \le {\rm{3}}\end{array} \right.\). Tính tích phân \(\int\limits_0^3 {f\left( x \right)dx} \).
A. \(6 + \ln 4\)
B. \(4 + \ln 4\)
C. \(6 + \ln 2\)
D. \(2 + 2\ln 2\)
Câu 10. Biết \(\int\limits_{\frac{1}{3}}^1 {\frac{{x - 5}}{{2x + 2}}dx} = a + \ln b\), với a, b là các số thực. Mệnh đề nào dưới đây đúng?
A. \(ab = \frac{8}{{81}}\) B. \(a + b = \frac{7}{{24}}\)
C. \(ab = \frac{9}{8}\) D. \(a + b = \frac{3}{{10}}\)
Câu 11. Tính tích phân \(\int\limits_1^2 {\frac{{ax + 1}}{{{x^2} + 3x + 2}}dx} = \frac{3}{5}\ln \frac{4}{3} + \frac{3}{5}\ln \frac{2}{3}\). Giá trị của a là:
A. \(a = \frac{1}{5}\) B. \(a = \frac{2}{5}\)
C. \(a = \frac{3}{5}\) D. \(a = \frac{4}{5}\)
Câu 12. Cho \(\int\limits_0^1 {\frac{x}{{\sqrt {3x + 1} + \sqrt {2x + 1} }}dx} = \frac{{a + b\sqrt 3 }}{9}\), với a, b là các số thực. Tính tổng \(T = a + b\)
A. \(T = - 10\)
B. \(T = - 4\)
C. \(T = 15\)
D. \(T = 8\)
Câu 13. Biết \(\int\limits_0^{\frac{\pi }{6}} {\left( {3 + 4{{\sin }^2}x} \right)dx} = \frac{{a\pi }}{b} - \frac{{c\sqrt 3 }}{6}\), trong đó a, b nguyên dương và \(\frac{a}{b}\) tối giản. Tính a+b+c.
A. 8 B. 16 C. 12 D. 14
Câu 14. Cho \(F\left( x \right) = \int\limits_0^{{x^2}} {{e^{{t^2}}}dt} \). Tính \(F'\left( 2 \right)\).
A. \(F'\left( 2 \right) = 4{e^4}\)
B. \(F'\left( 2 \right) = 8{e^{16}}\)
C. \(F'\left( 2 \right) = 4{e^{16}}\)
D. \(F'\left( 2 \right) = {e^4}\)
Câu 15. Cho hàm số \(g\left( x \right) = \int\limits_x^{{x^2}} {\frac{1}{{\ln t}}dt} \) với \(x > 0\). Đạo hàm của \(g\left( x \right)\) là:
A. \(g'\left( x \right) = \frac{{x - 1}}{{\ln x}}\)
B. \(g'\left( x \right) = \frac{{1 - x}}{{\ln x}}\)
C. \(g'\left( x \right) = \frac{1}{{\ln x}}\)
D. \(g'\left( x \right) = \ln x\)
Câu 16. Trong các tích phân sau, tích phân nào có cùng giá trị với \(I = \int\limits_1^2 {{x^3}\sqrt {{x^2} - 1} dx} \)
A. \(\frac{1}{2}\int\limits_1^2 {t\sqrt {t - 1} dt} \)
B. \(\int\limits_1^4 {t\sqrt {t - 1} dt} \)
C. \(\int\limits_0^{\sqrt 3 } {t\sqrt {t - 1} dt} \)
D. \(\int\limits_1^{\sqrt 3 } {\left( {{x^2} + 1} \right){x^2}dt} \)
Câu 17. Giả sử \(I = \int\limits_1^{64} {\frac{{dx}}{{\sqrt x + \sqrt[3]{x}}}} = a\ln \frac{2}{3} + b\) với a, b là số nguyên. Tính giá trị \(a - b\).
A. \( - 17\) B. \(5\)
C. \( - 5\) D. \(17\)
Câu 18. Tính tích phân \(I = \int\limits_0^{\frac{\pi }{3}} {\frac{{\sin x}}{{{{\cos }^3}x}}dx} \).
A. \(I = \frac{5}{2}\) B. \(I = \frac{3}{2}\)
C. \(I = \frac{\pi }{3} + \frac{9}{{20}}\) D. \(I = \frac{9}{4}\)
Câu 19. Cho \(I = \int\limits_0^1 {x.{e^{1 - {x^2}}}dx} \). Biết rằng \(I = \frac{{ae - b}}{2}\). Khi đó \(a + b\) bằng:
A. \(1\) B. 0 C. 2 D. 4
Câu 20. Biết \(\int\limits_1^2 {\frac{{x + 1}}{{{x^2} + x\ln x}}dx} = \ln \left( {\ln a + b} \right)\) với a, b là các số nguyên dương. Tính \(P = {a^2} + {b^2} + ab\).
A. 10 B. 8 C. 12 D. 6
Phần 3
Ứng dụng tích phân tính diện tích, thể tích.
Câu 1. Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục Ox và các đường thẳng \(x = a,x = b\left( {a < b} \right)\).
A. \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
B. \(\int\limits_a^b {{f^2}\left( x \right)dx} \)
C. \(\int\limits_a^b {f\left( x \right)dx} \)
D. \(\pi \int\limits_a^b {f\left( x \right)dx} \)
Câu 2. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên dưới.
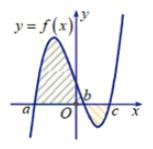
Hình phẳng được đánh dấu trong hình vẽ bên có diện tích là:
A. \(\int\limits_a^b {f\left( x \right)dx} - \int\limits_b^c {f\left( x \right)dx} \)
B. \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} \)
C. \( - \int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} \)
D. \(\int\limits_a^b {f\left( x \right)dx} - \int\limits_c^b {f\left( x \right)dx} \)
Câu 3. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^2} + x - 2\) và trục hoành bằng:
A. 9 B. \(\frac{{13}}{6}\) C. \(\frac{9}{2}\) D. \(\frac{3}{2}\)
Câu 4. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3} - 3{x^2}\), trục hoành và hai đường thẳng \(x = 1,x = 4\)là:
A. \(\frac{{53}}{4}\) B. \(\frac{{51}}{4}\)
C. \(\frac{{49}}{4}\) D. \(\frac{{25}}{2}\)
Câu 5. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \frac{{x + 1}}{{x - 2}}\) và các trục tọa độ Ox, Oy ta được \(S = a\ln \frac{b}{c} - 1\). Chọn đáp án đúng?
A. \(a + b + c = 8\)
B. \(a > b\)
C. \(a - b + c = 1\)
D. \(a + 2b - 9 = c\)
Câu 6. Biết diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = 3{x^2} + 2mx + {m^2} + 1\), trục hoành, trục tung và đường thẳng \(x = \sqrt 2 \) đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng?
A. \(m \in \left( { - 4; - 1} \right)\) B. \(m \in \left( {3;5} \right)\)
C. \(m \in \left( {0;3} \right)\) D. \(m \in \left( { - 2;1} \right)\)
Câu 7. Cho (H) là hình phẳng được giới hạn bởi các đường \(y = \sqrt x ,y = x - 2\) và trục hoành. Diện tích của (H) bằng:
A. \(\frac{7}{3}\) B. \(\frac{8}{3}\)
C. \(\frac{{10}}{3}\) D. \(\frac{{16}}{3}\)
Câu 8. Diện tích hình phẳng được giới hạn bởi các đường thẳng \(y = \left\{ \begin{array}{l} - x{\rm{ khi }}x \le 1\\x - 2{\rm{ khi }}x > 1\end{array} \right.\) và \(y = \frac{{10}}{3}x - {x^2}\) là \(\frac{a}{b}\). Khi đó \(a + 2b\) bằng:
A. 16 B.15 C. 17 D. 18
Câu 9. Cho (H) là hình phẳng được giới hạn bởi parabol \(y = \frac{{\sqrt 3 }}{2}{x^2}\) và đường Elip có phương trình \(\frac{{{x^2}}}{4} + {y^2} = 1\). Diện tích của (H) bằng
A. \(\frac{{2\pi + \sqrt 3 }}{6}\)
B. \(\frac{{2\pi }}{3}\)
C. \(\frac{{\pi + \sqrt 3 }}{4}\)
D. \(\frac{{3\pi }}{4}\)
Câu 10. Diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số \(x - {y^3} + 1 = 0,x + y - 1 = 0\) là
A. \(\frac{5}{4}\) B. \(\frac{1}{3}\)
C. \(\sqrt 2 \) D. Đáp án khác
Câu 11. Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^4} - 5{x^2} + 4\), trục hoành và hai đường thẳng \(x = 0,x = 1\).
A. \(\frac{7}{3}\) B. \(\frac{8}{5}\)
C. \(\frac{{64}}{{25}}\) D. \(\frac{{38}}{{15}}\)
Câu 12. Cho D giới hạn bởi các đường cong \(y = \sqrt {{x^2} + 1} \), trục hoành và các đường thẳng \(x = 0,x = 1\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
A. \(V = \frac{4}{3}\) B. \(V = 2\pi \)
C. \(V = \frac{{4\pi }}{3}\) D. \(V = 2\).
Câu 13. Cho hình cong (H) giới hạn bởi đường \(y = {e^x}\), trục hoành và các đường thẳng \(x = 0,x = \ln 4\). Đường thẳng x=k (0< x< ln4) chia (H) thành hai phần có diện tích là \({S_1}\) và \({S_2}\) như hình vẽ bên.
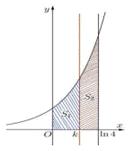
Tìm k để \({S_1} = 2{S_2}\).
A. \(k = \frac{2}{3}\ln 4\)
B. \(k = \ln 2\)
C. \(k = \ln \frac{8}{3}\)
D. \(k = \ln 3\)
Câu 14. Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - 1\) và \(y = - {x^2} + 2x + 3\) không được tính bằng công thức nào sau đây?
A. \(S = \int\limits_2^{ - 1} {\left( {2{x^2} - 2x - 4} \right)dx} \).
B. \(S = \int\limits_{ - 1}^2 {\left| {2{x^2} - 2x - 4} \right|dx} \)
C. \(S = \int\limits_{ - 1}^2 {\left| {\left( {{x^2} - 1} \right) - \left( { - {x^2} + 2x + 3} \right)} \right|dx} \)
D. \(S = \int\limits_{ - 1}^2 {\left( { - {x^2} - x + 2} \right)} \).
Câu 15. Cho hình (H) giới hạn bởi các đường \(y = \sqrt x ,x = 4\) và trục hoành. Quay hình (H) quanh trục Ox ta được khối tròn xoay có thể tích là bao nhiêu?
A. \(\frac{{15\pi }}{2}\) B. \(\frac{{14\pi }}{3}\)
C. \(8\pi \) D. \(\frac{{16\pi }}{3}\)
Phần 4
Số phức
Câu 1. Số phức nào sau đây là số thuần ảo
A. \(z = \sqrt 3 + i\)
B. \(z = - 2\)
C. \(z = - 2 + 3i\)
D. \(z = 3i\)
Câu 2. Tìm mô đung của số phức \(z = - 4i\) :
A. 4 B. - 4 C. \(\sqrt 4 \) D. \({4^2}\)
Câu 3. Cho các điểm A, B, C nằm trong mặt phẳng phức lần lượt biểu diễn các số phức \(1 + 3i, - 2 + 2i,1 - 7i\). Gọi D là điểm sao cho tứ giác ABCD là hình bình hành. Điểm D biểu diễn số phức nào trong các số phức sau đây?
A. \(z = 4 + 6i\)
B. \(z = 2 + 8i\)
C. \(z = - 2 - 8i\)
D. \(4 - 6i\)
Câu 4. Cho hai số phức \({z_1} = 2 + i,{z_2} = 1 + 3i\). Phần thực của số phức \({z_1} + {z_2}\) bằng:
A. 1 B. 3 C. 4 D. -2
Câu 5. Tính mô đun của số phức z biết \(\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right)\)
A. \(\left| z \right| = 5\sqrt 2 \)
B. \(\left| z \right| = \sqrt 2 \)
C. \(\left| z \right| = 25\sqrt 2 \)
D. \(\left| z \right| = 7\sqrt 2 \)
Câu 6. Cho số phức \(z = \frac{{\left( {2 - 3i} \right)\left( {4 - i} \right)}}{{3 + 2i}}\). Tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy.
A. \(\left( {1;4} \right)\) B. \(\left( { - 1;4} \right)\)
C. \(\left( { - 1; - 4} \right)\) D. \(\left( {1; - 4} \right)\)
Câu 7. Tìm hai số thực x và y thỏa mãn \(\left( {3x + yi} \right)\left( {4 - 2i} \right) = 5x + 2i\) với i là đơn vị ảo.
A. \(x = 2;y = 4\)
B. \(x = - 2;y = 0\)
C. \(x = 2;y = 0\)
D. \(x = - 2;y = 4\)
Câu 8. Có bao nhiêu số phức đồng thời thỏa mãn \(\left| z \right| = \sqrt {10} \) đồng thời phần ảo gấp 3 lần phần thực
A. 1 B. 2 C. 3 D. 4
Câu 9. Gọi A và B lần lượt là hai điểm biểu diễn của hai số phức \(z = 5 + 3i\) và \(z' = 3 + 5i\). Kết luận nào sau đây là đúng?
A. A và B đối xứng nhau qua trục hoành
B. A và B đối xứng nhau qua trục tung
C. A và B đối xứng nhau qua gốc tọa độ
D. A và B đối xứng nhau qua đường thẳng \(y = x\)
Câu 10. Cho số phức \(z\) thỏa mãn \(\frac{{5\left( {\overline z + i} \right)}}{{z + 1}} = 2 - i\). Mô đung của số phức \(\omega = 1 + z + {z^2}\) là
A. \(4\) B. 9 C. 13 D. \(\sqrt {13} \)
A.
Câu 11. Cho số phức z thỏa mãn \(\left| {z - 1} \right| = 2\). Biết rằng tập hợp điểm biểu diễn các số phức \({\rm{w}} = \left( {1 + i\sqrt 3 } \right)z + 2\) là một đường tròn. Tính bán kính r của đường tròn đó.
A. \(r = 16\)
B. \(r = 4\)
C. \(r = 25\)
D. \(r = 9\)
Câu 12. Tập hợp các điểm biểu diễn cho số phức z thỏa mãn \(2\left| {z - i} \right| = \left| {z - \overline z + 2i} \right|\) là
A. Một đường thẳng
B. Một đường tròn
C. Một Parabol
D. Một Elip
Câu 13. Tìm phần thực, phần ảo của số phức z thỏa mãn \(\left( {\frac{z}{2} - i} \right)\left( {1 - i} \right) = {\left( {1 + i} \right)^{3979}}\)?
A. Phần thực là \({2^{1990}}\) và phần ảo là 2
B. Phần thực là \( - {2^{1990}}\) và phần ảo là 2
C. Phần thực là \( - {2^{1989}}\) và phần ảo là 1
D. Phần thực là \({2^{1989}}\) và phần ảo là 1
Câu 14. Phương trình \(\left( {2 + i} \right){z^2} + az + b = 0\left( {a,b \in \mathbb{C}} \right)\) có hai nghiệm là \(3 + i\) và \(1 - 2i\). Khi đó a=?
A. \( - 9 - 2i\)
B. \(15 + 5i\)
C. \(9 + 2i\)
D. \(15 - 5i\)
Câu 15. Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ?
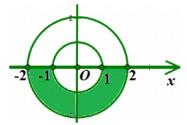
A. \(1 \le \left| z \right| \le 2\) và phần ảo dương.
B. \(1 \le \left| z \right| \le 2\) và phần ảo âm.
C. \(1 < \left| z \right| < 2\) và phần ảo dương.
D. \(1 < \left| z \right| < 2\) và phần ảo âm.
Phần 5
Hệ trục tọa độ
Câu 1. Cho vecto \(\overrightarrow {AO} = 3\left( {\overrightarrow i + 4\overrightarrow j } \right) - 2\overrightarrow k + 5\overrightarrow j \). Tọa độ của điểm A là:
A. (3;-2;5)
B. (-3;-17;2)
C. (3;17;-2)
D. (3;5;-2)
Câu 2. Cho \(\overrightarrow m = \left( {1;0; - 1} \right),\overrightarrow n = \left( {0;1;1} \right)\). Kết luận nào sai?
A. \(\overrightarrow m .\overrightarrow n = - 1\)
B. \(\left[ {\overrightarrow m ,\overrightarrow n } \right] = \left( {1; - 1;1} \right)\)
C. \(\overrightarrow m \) và \(\overrightarrow n \) không cùng phương
D. Góc của \(\overrightarrow m \) và \(\overrightarrow n \)là \(60^\circ \)
Câu 3. Cho \(\overrightarrow a \) và \(\overrightarrow b \) tạo với nhau một góc \(\frac{{2\pi }}{3}\). Biết \(\left| {\overrightarrow a } \right| = 3,\left| {\overrightarrow b } \right| = 5\) thì \(\left| {\overrightarrow a - \overrightarrow b } \right|\) bằng
A. 6 B. 5 C. 4 D. 7
Câu 4. Cho hai vecto \(\overrightarrow a = \left( {1;m; - 1} \right),\overrightarrow b = \left( {2;1;3} \right)\). \(\overrightarrow a \bot \overrightarrow b \) khi:
A. \(m = - 1\)
B. \(m = 1\)
C. \(m = 2\)
D. \(m = - 2\)
Câu 5. Cho ba vevto \(\overrightarrow a = \left( { - 1;0; - 2} \right)\), \(\overrightarrow b = \left( {1;2;1} \right)\), \(\overrightarrow c = \left( {4;3;m} \right)\). Để ba vecto trên đồng phẳng thì m bằng:
A. 14 B. 5 C. -7 D. 7
Câu 6. Cho 3 điểm \(M\left( {2;3; - 1} \right),N\left( { - 1;1;1} \right),P\left( {1;m - 1;2} \right)\). Tìm M để \(\Delta MNP\) vuông tại N.
A. 3 B. 2 C. 1 D. 0
Câu 7. Cho điểm \(M\left( {3;1; - 2} \right)\). Điểm N đối xứng với M qua Ox có tọa độ là:
A. \(\left( { - 3;1;2} \right)\)
B. \(\left( { - 3; - 1; - 2} \right)\)
C. \(\left( {3;1;0} \right)\)
D. \(\left( {3; - 1;2} \right)\)
Câu 8. Cho \(A\left( {4;2;6} \right)\), \(B\left( {10; - 2;4} \right),C\left( {4; - 4;0} \right),D\left( { - 2;0;2} \right)\). Tứ giác ABCD là hình:
A. Bình hành
B. Vuông
C. Chữ nhật
D. Thoi
Câu 9. Cho \(\overrightarrow a \left( {3;2;1} \right),\overrightarrow b \left( { - 2;0;1} \right)\). Độ dài của \(\overrightarrow a + \overrightarrow b \) bằng
A. 1 B. 2 C. 3 D. \(\sqrt 2 \)
Câu 10. Cho ba điểm \(A\left( {2; - 1;5} \right)\), \(B\left( {5; - 5;7} \right),M\left( {x;y;1} \right)\). Tìm x, y để A, B, M thẳng hàng?
A. x = 4,y = 7
B. x = - 4, y = - 7
C. x = 4, y = - 7
D. x = - 4, y = 7
Câu 11. Cho 3 điểm \(A\left( {2;5; - 1} \right),B\left( {2;2;3} \right),C\left( { - 3;2;3} \right)\). Mệnh đề nào sau đây sai?
A. \(\Delta ABC\) đều.
B. A, B, C không thẳng hàng
C. \(\Delta ABC\) vuông
D.\(\Delta ABC\) cân tại B.
Câu 12. Cho 4 điểm \(A\left( {1;0;0} \right),B\left( {0;1;0} \right),C\left( {0;0;1} \right),D\left( {1;1;1} \right)\). Mệnh đề nào sai?
A. 4 điểm A, B, C, D tạo thàng 1 tứ diện
B. \(\Delta ABD\) đều
C. \(AB \bot CD\)
D. \(\Delta BCD\) vuông.
Câu 13. Cho \(A\left( {0;2; - 2} \right),B\left( { - 3;1; - 1} \right)\), \(C\left( {4;3;0} \right)\), \(D\left( {1;2;m} \right)\). Tìm m để A, B, C, D đồng phẳng:
A. \( - 5\)
B. \( - 1\)
C. 1
D. 5
Câu 14. Trong không gian Oxyz, cho \(\overrightarrow u = \left( {1;1; - 2} \right),\overrightarrow v = \left( {1;0;m} \right)\). Tìm m để góc giữa hai vecto \(\overrightarrow u ,\overrightarrow v \) bằng \(45^\circ \)
A. m=2
B. \(m = 2 - \sqrt 6 \)
C. \(m = 2 + \sqrt 6 \)
D. \(m = 2 \pm \sqrt 6 \)
Câu 15. Trong không gian Oxyz, cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {1;1; - 6} \right),B\left( {0;0; - 2} \right),\)\(C\left( { - 5;1;2} \right),D'\left( {2;1; - 1} \right)\). Thể tích khối hộp đã cho bằng.
A. 42 B. 19 C. 38 D. 12.
Phần 6
Phương trình mặt phẳng
Câu 1. Vecto nào sau đây là vecto pháp tuyến của mặt phẳng \(\left( P \right):4x - 3y + 1 = 0\).
A. \(\left( {4; - 3;0} \right)\)
B. \(\left( {4; - 3;1} \right)\)
C. \(\left( {4; - 3; - 1} \right)\)
D. \(\left( { - 3;4;0} \right)\)
Câu 2. Phương trình mặt phẳng (P) chứa điểm \(M\left( { - 1;2;0} \right)\) và có veto pháp tuyến \(\overrightarrow n = \left( {4;0; - 5} \right)\) là:
A. \(4x - 5y - 4 = 0\)
B. \(4x - 5z - 4 = 0\)
C. \(4x - 5y + 4 = 0\)
D. \(4x - 5z + 4 = 0\)
Câu 3. Mặt phẳng song song với hai đường thẳng \({\Delta _1}:\frac{{x - 2}}{2} = \frac{{y + 1}}{{ - 3}} = \frac{z}{4},\)\({\Delta _2}:\left\{ \begin{array}{l}x = 2 + t\\y = 3 + 2t\\z = 1 - t\end{array} \right.\) có một vecto pháp tuyến là:
A. \(\overrightarrow n = \left( { - 5;6; - 7} \right)\)
B. \(\overrightarrow n = \left( {5 - ;6;7} \right)\)
C. \(\overrightarrow n = \left( { - 5; - 6;7} \right)\)
D. \(\overrightarrow n = \left( { - 5;6;7} \right)\)
Câu 4. Cho hai điểm \(A\left( { - 2;0;1} \right),B\left( {4;2;5} \right)\). Phương trình mặt phẳng trung trục của AB là:
A. \(3x + y + 2z - 10 = 0\)
B. \(3x + y + 2z + 10 = 0\)
C. \(3x + y - 2z - 10 = 0\)
D. \(3x - y + 2z - 10 = 0\)
Câu 5. Cho \(\left( Q \right):3x - y - 2z + 1 = 0\), (P) song song với (Q), chứa \(A\left( {0;0;1} \right)\) có phương trình là:
A. \(3x - y - 2z + 2 = 0\)
B. \(3x - y - 2z - 2 = 0\)
C. \(3x - y - 2z + 3 = 0\)
D. \(3x - y - 2z + + 5 = 0\)
Câu 6. Mặt phẳng (P) song song với Oxy và đi qua \(A\left( {1; - 2;1} \right)\) có phương trình là
A.\(z - 1 = 0\)
B. \(x - 2y + z = 0\)
C. \(x - 1 = 0\)
D. \(y + 2 = 0\)
Câu 7. Cho hai mặt phẳng \(\left( \alpha \right):3x - 2y + 2z + 7 = 0\) và \(\left( \beta \right):5x - 4y + 3z + 1 = 0\). Phương trình mặt phẳng đi qua gốc tọa độ O và vuông góc cả \(\left( \alpha \right),\left( \beta \right)\) là
A. \(2x - y + 2z = 0\)
B. \(2x + y - 2z = 0\)
C. \(2x + y - 2z + 1 = 0\)
D. \(2x - y - 2z = 0\)
Câu 8. Trong không gian Oxyz, phương trình mặt phẳng (Oxy) là
A. \(z = 0\)
B. \(x + y = 0\)
C. \(x = 0\)
D. \(y = 0\)
Câu 9. Mặt phẳng (P) chứa \(A\left( {1; - 2;3} \right)\), vuông góc với \(\left( d \right):\frac{{x + 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 1}}{3}\) có phương trình là:
A. \(2x - y + 3z - 13 = 0\)
B. \(2x - y + 3z + 13 = 0\)
C. \(2x - y - 3z - 13 = 0\)
D. \(2x + y + 3z - 13 = 0\)
Câu 10. Mặt phẳng đi qua \(D\left( {2;0;0} \right)\) vuông góc với trục Oy có phương trình là:
A.\(z = 0\).
B. \(y = 2\)
C. \(y = 0\)
D. \(z = 2\)
Câu 11. Cho 2 điểm \(A\left( { - 1;0;0} \right),B\left( {0;0;1} \right)\). Mặt phẳng (P) chứa đường thẳng AB và song song với trục O có phương trình là
A.\(x - z + 1 = 0\)
B. \(x - z - 1 = 0\)
C. \(x + y - z + 1 = 0\)
D. \(y - z + 1 = 0\)
Câu 12. Mặt phẳng (P) chứa Oz và đi qua \(A\left( {1;2;3} \right)\) có phương trình là:
A. \(2x - y = 0\)
B. \(x + y - z = 0\)
C. \(x - y + 1 = 0\)
D. \(x - 2y + z = 0\)
Câu 13. Trong không gian Oxyz cho mặt phẳng \(\left( Q \right):3x + 4y - 1 = 0\). Mặt phẳng (P) song song với (Q) và cách gốc tọa độ một khoảng bằng 1 có phương trình là:
A. \(3x + 4y + 5 = 0\) hoặc \(3x + 4y - 5 = 0\)
B. \(3x + 4y + 5 = 0\)
C. \(3x + 3y - 5 = 0\)
D. \(4x + 3y + 5 = 0\) hoặc \(3x + 4y + 5 = 0\)
Câu 14. Mặt phẳng (P) đi qua \(M\left( {1;2;2} \right)\) và cắt trục Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình của (P) là:
A. \(2x + y + z - 4 = 0\)
B. \(2x + y + z - 2 = 0\)
C. \(2x + 4y + 4z - 9 = 0\)
D. \(x + 2y + 2z - 9 = 0\)
Câu 15. Viết phương trình mặt phẳng (P) biết (P) cắt ba trục tọa độ lần lượt tại A, B, C sao cho \(M\left( {1;2;3} \right)\) làm trọng tâm tam giác ABC:
A. \(6x + 3y + 2z - 18 = 0\)
B. \(x + 2y + 3z = 0\)
C. \(6x - 3y + 2z - 18 = 0\)
D. \(6x + 3y + 2z + 18 = 0\)
Phần 7
Phương trình đường thẳng
Câu 1. Cho đường thẳng d đi qua \(M\left( {2;0; - 1} \right)\) và có vecto chỉ phương \(\overrightarrow a \left( {4; - 6;2} \right)\). Phương trình tham số của đường thẳng d là:
A. \(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3t\\z = 1 + t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3t\\z = - 1 + t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 6 - 3t\\z = 2 + t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 2 + 4t\\y = - 6t\\z = 1 + 2t\end{array} \right.\)
Câu 2. Phương trình đường thẳng AB với \(A\left( {1;1;2} \right),B\left( {2; - 1;0} \right)\) là:
A. \(\frac{{x - 1}}{3} = \frac{{y - 1}}{2} = \frac{{z - 2}}{2}\)
B. \(\frac{{x + 1}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z + 2}}{2}\)
C. \(\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 2}} = \frac{z}{3}\)
D. \(\frac{x}{1} = \frac{{y - 3}}{{ - 2}} = \frac{{z - 4}}{{ - 2}}\)
Câu 3. Cho đường thẳng d đi qua điểm \(A\left( {1;2;3} \right)\) và vuông góc với mặt phẳng \(\left( \alpha \right):4x + 3y - 7z + 1 = 0\). Phương trình tham số của d là:
A. \(\left\{ \begin{array}{l}x = 1 + 4t\\y = 2 + 3t\\z = 3 - 7t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = - 1 + 8t\\y = - 2 + 6t\\z = - 3 - 14t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 - 4t\\z = 3 - 7t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 1 + 4t\\y = - 2 + 3t\\z = - 3 - 7t\end{array} \right.\)
Câu 4. Cho \(A\left( {0;0;1} \right),B\left( { - 1; - 2;0} \right),C\left( {2;1; - 1} \right)\). Đường thẳng \(\Delta \) đi qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng \(\left( {ABC} \right)\) có phương trình.
A. \(\left\{ \begin{array}{l}x = \frac{1}{3} + 5t\\y = - \frac{1}{3} + 4t\\z = 3t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = \frac{1}{3} + 5t\\y = - \frac{1}{3} - 4t\\z = 3t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = \frac{1}{3} - 5t\\y = - \frac{1}{3} - 4t\\z = - 3t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = \frac{1}{3} - 5t\\y = - \frac{1}{3} - 4t\\z = 3t\end{array} \right.\)
Câu 5. Cho hai mặt phẳng \(\left( P \right):2x + y - z - 3 = 0\)và \(\left( Q \right):x + y + z - 1 = 0\). Phương trình chính tắc của đường thẳng giao tuyến của 2 mặt phẳng (P) và (Q) là:
A. \(\frac{x}{2} = \frac{{y - 2}}{{ - 3}} = \frac{{z + 1}}{1}\)
B. \(\frac{{x + 1}}{{ - 2}} = \frac{{y - 2}}{{ - 3}} = \frac{{z - 1}}{1}\)
C. \(\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z + 1}}{1}\)
D. \(\frac{x}{2} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 1}}{{ - 1}}\)
Câu 6. Trong không gian Oxyz, cho tam giác ABC với \(A\left( {1; - 3;4} \right),B\left( { - 2; - 5; - 7} \right)\) và \(C\left( {6; - 3; - 1} \right)\). Phương trình đường trung tuyến AM của tam giác ABC là:
A. \(\frac{{x - 1}}{3} = \frac{{y + 3}}{4} = \frac{{z - 4}}{{ - 1}}\)
B. \(\frac{{x - 1}}{3} = \frac{{y + 3}}{{ - 2}} = \frac{{z - 4}}{{ - 11}}\)
C. \(\frac{{x - 1}}{1} = \frac{{y + 1}}{{ - 3}} = \frac{{z + 8}}{{ - 4}}\)
D. \(\frac{{x - 1}}{1} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{{ - 8}}\)
Câu 7. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng có phương trình \(d:\frac{{x - 2}}{1} = \frac{{y - 1}}{1} = \frac{{z - 1}}{{ - 1}}\) và mặt phẳng \(\left( P \right):x + my + \left( {{m^2} - 1} \right)z - 7 = 0\). Tìm m để đường thẳng d song song với (P).
A. \(m = - 1\)
B. \(m = 1\) hoặc \(m = - 2\)
C. \(m = - 2\)
D. \(m = 2\) hoặc \(m = - 1\)
Câu 8. Trong không gian Oxyz, cho hai đường thẳng \(\left( {{\Delta _1}} \right):\left\{ \begin{array}{l}x = - 3 + 2t\\y = 1 - t\\z = - 1 + 4t\end{array} \right.\) và \(\left( {{\Delta _2}} \right):\frac{{x + 4}}{3} = \frac{{y + 2}}{2} = \frac{{z - 4}}{{ - 1}}\). Khẳng định nào sau đây đúng?
A. \(\left( {{\Delta _1}} \right)//\left( {{\Delta _2}} \right)\)
B. \(\left( {{\Delta _1}} \right)\) và \(\left( {{\Delta _2}} \right)\) chéo và vuông góc với nhau
C. \(\left( {{\Delta _1}} \right)\) cắt và không vuông góc với \(\left( {{\Delta _2}} \right)\)
D. \(\left( {{\Delta _1}} \right)\) cắt và vuông góc với \(\left( {{\Delta _2}} \right)\)
Câu 9. Trong không gian Oxyz, cho điểm \(M\left( {1; - 3;4} \right)\), đường thẳng \(d:\frac{{x + 2}}{3} = \frac{{y - 5}}{{ - 5}} = \frac{{z - 2}}{{ - 1}}\) và mặt phẳng \(\left( P \right):2x + z - 2 = 0\). Viết phương trình đường thẳng \(\Delta \) qua M vuông góc với d và song song với (P).
A. \(\Delta :\frac{{x - 1}}{1} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{{ - 2}}\)
B. \(\Delta :\frac{{x - 1}}{1} = \frac{{y + 3}}{1} = \frac{{z - 4}}{{ - 2}}\)
C. \(\Delta :\frac{{x - 1}}{{ - 1}} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{{ - 2}}\)
D. \(\Delta :\frac{{x - 1}}{1} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{2}\)
Câu 10. Trong không gian Oxyz, cho đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( P \right):z - 1 = 0\) và \(\left( Q \right):x + y + z - 3 = 0\). Gọi d là đường thẳng nằm trong mặt phẳng (P), cắt đường thẳng \(\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{{ - 1}}\) và vuông góc với đường thẳng \(\Delta \). Phương trình của đường thẳng d là:
A. \(\left\{ \begin{array}{l}x = 3 + t\\y = t\\z = 1 + t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = 3 - t\\y = t\\z = 1\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 3 + t\\y = t\\z = 1\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = 3 + t\\y = - t\\z = 1 + t\end{array} \right.\)
Phần 8
Phương trình mặt cầu
Câu 1. Phương trình nào sau đây là phương trình mặt cầu ?
A.\({x^2} + {y^2} + {z^2} - 2x = 0.\)
B. \({x^2} + {y^2} - {z^2} + 2x - y + 1 = 0.\)
C. \(2{x^2} + 2{y^2} = {\left( {x + y} \right)^2} - {z^2} + 2x - 1.\)
D. \({\left( {x + y} \right)^2} = 2xy - {z^2} - 1.\)
Câu 2. Phương trình nào sau đây không phải là phương trình mặt cầu ?
A. \({x^2} + {y^2} + {z^2} - 2x = 0.\)
B. \(2{x^2} + 2{y^2} = {\left( {x + y} \right)^2} - {z^2} + 2x - 1.\)
C. \({x^2} + {y^2} + {z^2} + 2x - 2y + 1 = 0.\)
D. \({\left( {x + y} \right)^2} = 2xy - {z^2} + 1 - 4x.\)
Câu 3. Phương trình nào sau đây không phải là phương trình mặt cầu ?
A. \({\left( {x - 1} \right)^2} + {\left( {2y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 6.\)
B. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 6.\)
C. \({\left( {2x - 1} \right)^2} + {\left( {2y - 1} \right)^2} + {\left( {2z + 1} \right)^2} = 6.\)
D. \({\left( {x + y} \right)^2} = 2xy - {z^2} + 3 - 6x.\)
Câu 4. Cho các phương trình sau: \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = 1;\) \({x^2} + {\left( {2y - 1} \right)^2} + {z^2} = 4;\)
\({x^2} + {y^2} + {z^2} + 1 = 0;\) \({\left( {2x + 1} \right)^2} + {\left( {2y - 1} \right)^2} + 4{z^2} = 16.\)
Số phương trình là phương trình mặt cầu là:
A. 4. B. 3. C. 2. D. 1.
Câu 5. Mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {z^2} = 9\) có tâm là:
A. \(I\left( {1; - 2;0} \right).\)
B. \(I\left( { - 1;2;0} \right).\)
C. \(I\left( {1;2;0} \right).\)
D. \(I\left( { - 1; - 2;0} \right).\)
Câu 6. Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\) có tâm là:
A. \(I\left( {8; - 2;0} \right).\) B. \(I\left( { - 4;1;0} \right).\)
C. \(I\left( { - 8;2;0} \right).\) D. \(I\left( {4; - 1;0} \right).\)
Câu 7. Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 1 = 0\) có tọa độ tâm và bán kính R là:
A. \(I\left( {2;0;0} \right),{\rm{ }}R = \sqrt 3 .\)
B. \(I\left( {2;0;0} \right),{\rm{ }}R = 3.\)
C. \(I\left( {0;2;0} \right),{\rm{ }}R = \sqrt 3 .\)
D. \(I\left( { - 2;0;0} \right),{\rm{ }}R = \sqrt 3 .\)
Câu 8. Phương trình mặt cầu có tâm \(I\left( { - 1;2; - 3} \right)\), bán kính \(R = 3\) là:
A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 9.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 3.\)
C. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\)
D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\)
Câu 9. Mặt cầu \(\left( S \right):{\left( {x + y} \right)^2} = 2xy - {z^2} + 1 - 4x\) có tâm là:
A. \(I\left( { - 2;0;0} \right).\) B. \(I\left( {4;0;0} \right).\)
C. \(I\left( { - 4;0;0} \right).\) D. \(I\left( {2;0;0} \right).\)
Câu 10. Đường kính của mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z - 1} \right)^2} = 4\) bằng:
A. 4. B. 2. C. 8. D. 16.
Câu 11. Cho đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = - 1 + 3t\\z = 1\end{array} \right.\). Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của đường thẳng d và trục Ox là:
A.\({\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = \frac{1}{2}.\)
B.\({\left( {x + 1} \right)^2} + {y^2} + {\left( {z + 2} \right)^2} = \frac{1}{4}.\)
C. \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = \frac{1}{2}.\)
D. \({\left( {x - \frac{1}{3}} \right)^2} + {y^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{1}{4}.\)
Câu 12. Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 2t\\y = t\\z = 4\end{array} \right.\)và \(d':\left\{ \begin{array}{l}x = {t^'}\\y = 3 - t'\\z = 0\end{array} \right.\). Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của đường thẳng d và d’ là:
A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 4.\)
B. \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4.\)
C. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 2.\)
D.\({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 4.\)
Câu 13. Cho các điểm \(A\left( { - 2;4;1} \right)\) và \(B\left( {2;0;3} \right)\) và đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\). Gọi \(\left( S \right)\) là mặt cầu đi qua A, B và có tâm thuộc đường thẳng D. Bán kính mặt cầu (S) bằng:
A. \(\frac{{\sqrt {1169} }}{4}.\)B.\(\frac{{\sqrt {873} }}{4}.\)C. \(\frac{{1169}}{{16}}.\)D.\(\frac{{\sqrt {967} }}{2}.\)
Câu 14. Phương trình mặt cầu có tâm \(I\left( { - \sqrt 6 ; - \sqrt 3 ;\sqrt 2 - 1} \right)\) và tiếp xúc trục Oz là:
A.\({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 + 1} \right)^2} = 9.\)
B.\({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 - 1} \right)^2} = 9.\)
C. \({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 - 1} \right)^2} = 3.\)
D. \({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 + 1} \right)^2} = 3.\)
Câu 15. Phương trình mặt cầu có tâm \(I\left( {4;6; - 1} \right)\) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông là:
A.\({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 26.\)
B. \({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 74.\)
C. \({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 34.\)
D.\({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 104.\)
Câu 16. Phương trình mặt cầu có tâm \(I\left( {\sqrt 3 ; - \sqrt 3 ;0} \right)\) và cắt trục Oz tại hai điểm A, B sao cho tam giác IAB đều là:
A.\({\left( {x + \sqrt 3 } \right)^2} + {\left( {y - \sqrt 3 } \right)^2} + {z^2} = 8.\)
B.\({\left( {x - \sqrt 3 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {z^2} = 9.\)
C. \({\left( {x + \sqrt 3 } \right)^2} + {\left( {y - \sqrt 3 } \right)^2} + {z^2} = 9.\)
D. \({\left( {x - \sqrt 3 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {z^2} = 8.\)
Câu 17. Phương trình mặt cầu có tâm \(I\left( {3;6; - 4} \right)\) và cắt trục Oz tại hai điểm A, B sao cho diện tích tam giác IAB bằng \(6\sqrt 5 \) là:
A. \({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 49.\)
B.\({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 45.\)
C. \({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 36.\)
D.\({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 54.\)
Câu 18. Mặt cầu (S) có tâm \(I\left( {2;1; - 1} \right)\) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông. Điểm nào sau đây thuộc mặt cầu (S):
A. \(\left( {2;1;1} \right).\) B. \(\left( {2;1;0} \right).\)
C. \(\left( {2;0;0} \right).\) D. \(\left( {1;0;0} \right).\)
Câu 19. Gọi (S) là mặt cầu có tâm \(I\left( {1; - 3;0} \right)\) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB đều. Điểm nào sau đây không thuộc mặt cầu (S):
A. \(\left( { - 1; - 3;2\sqrt 3 } \right).\)
B. \(\left( {3; - 3;2\sqrt 2 } \right).\)
C. \(\left( {3; - 3; - 2\sqrt 2 } \right).\)
D. \(\left( {2; - 1;1} \right).\)
Câu 20. Cho các điểm \(I\left( { - 1;0;0} \right)\) và đường thẳng \(d:\frac{{x - 2}}{1} = \frac{{y - 1}}{2} = \frac{{z - 1}}{1}\). Phương trình mặt cầu \(\left( S \right)\) có tâm I và tiếp xúc d là:
A. \({\left( {x + 1} \right)^2} + {y^2} + {z^2} = 5.\)
B.\({\left( {x - 1} \right)^2} + {y^2} + {z^2} = 5.\)
C. \({\left( {x + 1} \right)^2} + {y^2} + {z^2} = 10.\)
D.\({\left( {x - 1} \right)^2} + {y^2} + {z^2} = 10.\)

