Đề bài
Giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(1\). Tính khoảng cách từ đỉnh \(A\) đến các mặt phẳng \((A'BD)\) và \((B'D'C)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Gắn hệ trục tọa độ sao cho \(A(0;0;0), B(1;0;0); D(0;1;0), A'(0;0;1).\)
+) Tìm tọa độ các đỉnh còn lại của hình lập phương.
+) Viết phương trình các mặt phẳng \((A'BD)\) và \((B'D'C)\).
+) Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng tính khoảng cách từ đỉnh \(A\) đến các mặt phẳng \((A'BD)\) và \((B'D'C)\).
Lời giải chi tiết
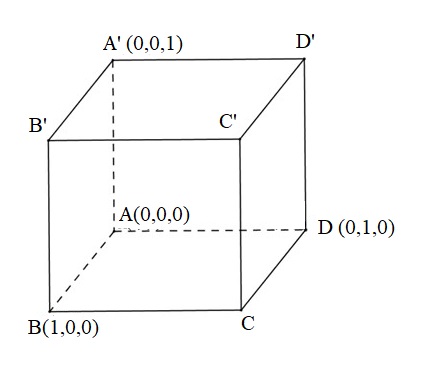
Chọn hệ trục tọa độ \(Oxyz\) sao cho \(A(0 ; 0 ; 0), B(1 ; 0 ; 0), D(0 ; 1; 0), A'(0 ; 0 ; 1)\)
Khi đó \(B'(1 ; 0 ; 1), D'(0 ; 1 ; 1), C(1 ; 1 ; 0)\).
Phương trình mặt phẳng \((A'BD)\) có dạng: \(\dfrac{x}{1} + \dfrac{y}{1} + \dfrac{z}{1} = 1 \) \(\Leftrightarrow x + y + z - 1 = 0\).
\(\overrightarrow{CB'}(0 ; -1 ; 1)\) ; \(\overrightarrow{CD'}(-1 ; 0 ; 1)\)
Mặt phẳng \((B'D'C)\) qua điểm \(C\) và nhận \(\overrightarrow{n}=\left [\overrightarrow{CB'},\overrightarrow{CD'} \right ] = (-1 ; -1 ; -1 )\) hay \(\overrightarrow {n}=(1;1;1)\) làm vectơ pháp tuyến
Phương trình mặt phẳng \((B'D'C)\) có dạng: \(x-1 + y-1 + z = 0 \) \(\Leftrightarrow x+y+z-2=0\)
Vậy:
\(\begin{array}{l}d\left( {A;\left( {A'BD} \right)} \right) = \dfrac{{\left| { - 1} \right|}}{{\sqrt {1 + 1 + 1} }} = \dfrac{1}{{\sqrt 3 }}\\d\left( {A;\left( {B'D'C} \right)} \right) = \dfrac{{\left| { - 2} \right|}}{{\sqrt {1 + 1 + 1} }} = \dfrac{2}{{\sqrt 3 }}\end{array}\)

