Đề bài
Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính quả bóng bàn. Gọi S1 là tổng diện tích của ba quả bóng bàn, S2 là diện tích xung quanh của hình trụ. Tỉ số \(\displaystyle{{{S_1}} \over {{S_2}}}\) bằng:
(A) 1 ; (B) 2 ;
(C) 1,5 ; (D) 1,2 .
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nhận xét: Bán kính của quả bóng bàn chính là bán kính đáy của hình trụ và chiều cao của hình trụ bằng ba lần đường kính của 1 quả bóng bàn.
Diện tích của một quả bóng bàn \(S = 4\pi {R^2} \Rightarrow {S_1} = 3S\).
Diện tích xung quanh của hình trụ: \(S_2 = 2\pi Rh\), trong đó \(R;h\) lần lượt là bán kính đáy và chiều cao của khối trụ.
Từ đó suy ra tỉ số \(\displaystyle{{{S_1}} \over {{S_2}}}\).
Lời giải chi tiết
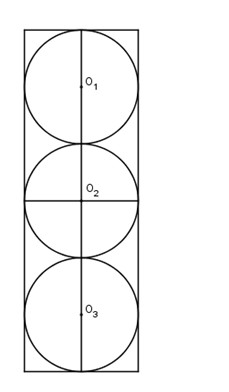
Gọi bán kính của quả cầu là \(r\) thì \(r\) cũng là bán kính đáy của hình trụ.
Chiều cao của hình trụ là \(h=3.2r=6r\)
Diện tích ba quả bóng bàn là: \({S_1} = 3.4\pi {r^2} = 12\pi {r^2}\)
Diện tích xung quanh của hình trụ là: \({S_2} =2\pi r.6r= 12\pi {r^2}\)
Vậy \(\dfrac{{{S_1}}}{{{S_2}}} = 1\).
Chọn (A).

