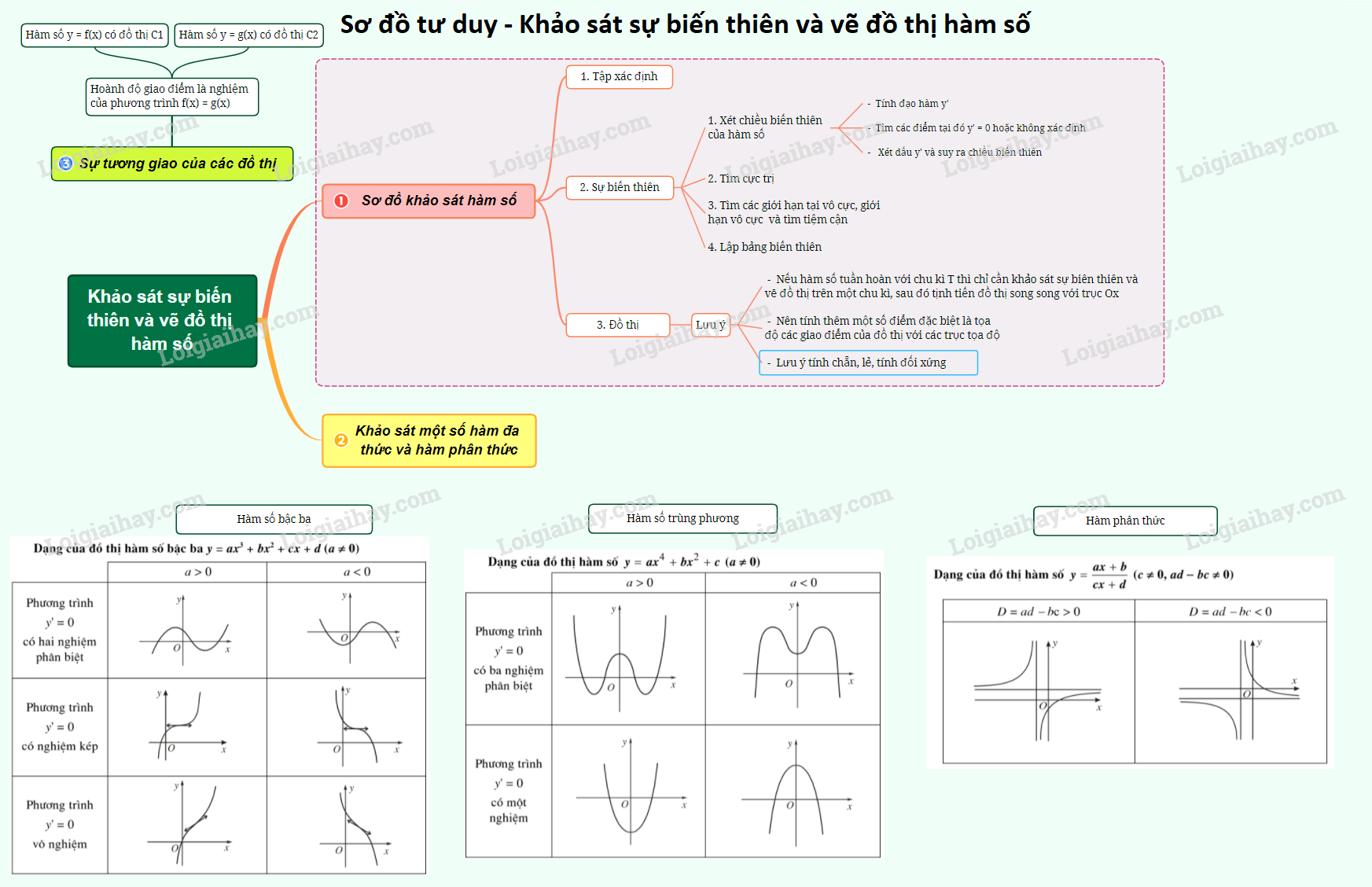
1. Các bước khảo sát và vẽ đồ thị hàm số y = f(x)
i) Tìm tập xác định của hàm số.
ii) Sự biến thiên
+ Xét sự biến thiên của hàm số
- Tìm đạo hàm bậc nhất \(y'\) ;
- Tìm các điểm tại đó \(y'\) bằng 0 hoặc không xác định ;
- Xét dấu \(y'\) và suy ra chiều biến thiên của hàm số.
+ Tìm cực trị.
+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).
+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị
iii) Vẽ đồ thị (thể hiện các cực trị, tiệm cận, giao của đồ thị với các trục, . . .)
2. Bảng tóm tắt một số dạng đồ thị thường gặp

3. Tương giao của các đồ thị
Cho hai đồ thị \((C_{1}):y=f(x);\) và \((C_{2}):y=g(x).\)
Phương trình xác định hoành độ giao điểm của \((C_{1})\) và \((C_{2})\) là: \(f(x)=g(x).\) (1)
- Nếu (1) vô nghiệm thì \((C_{1})\) và \((C_{2})\) không có điểm chung (không cắt nhau và không tiếp xúc với nhau).
- Nếu (1) có \(n\) nghiệm phân biệt thì \((C_{1})\) và \((C_{2})\) giao nhau tại \(n\) điểm phân biệt. Nghiệm của (1) chính là hoành độ các giao điểm.
Chú ý
a) \((C_{1})\) tiếp xúc với \((C_{2})\) \(\Leftrightarrow\) hệ \(\left\{ \begin{matrix} f(x) =g(x)& \\ f'(x)=g'(x) & \end{matrix}\right.\) có nghiệm. Nghiệm của hệ là hoành độ tiếp điểm của hai đồ thị đó.
b) Đường thẳng (d): y: mx+n tiếp xúc với parabol \(y = a{x^2} + bx + c\) (\(a\ne 0\))
\(\Leftrightarrow\) hệ \(\left\{ \begin{matrix} ax^{2}+bx+c=mx+n \\ 2ax+b=m \end{matrix}\right.\) có nghiệm
\(\Leftrightarrow\) phương trình \(ax^{2}+bx+c=mx+n\) có nghiệm kép.
Dành cho chương trình nâng cao
1. Chứng minh \((x_{0};y_{0})\) là tâm đối xứng của đồ thị (C) của hàm số y=f(x)
Đồ thị hàm số lẻ luôn nhận gốc tọa độ là tâm đối xứng.
Vậy để chứng minh \(I(x_{0};y_{0})\) là tâm đối xứng, ta dùng công thức đổi trục: \(\left\{\begin{matrix} x=x_{0}+X & \\ y=y_{0}+Y & \end{matrix}\right.\) để đưa hệ trục \(Oxy\) về hệ trục \(IXY\) (gốc \(I\)) và chứng minh: trong hệ trục \(IXY\), hàm số đã cho có dạng \(Y=g(X)\) là hàm số lẻ.
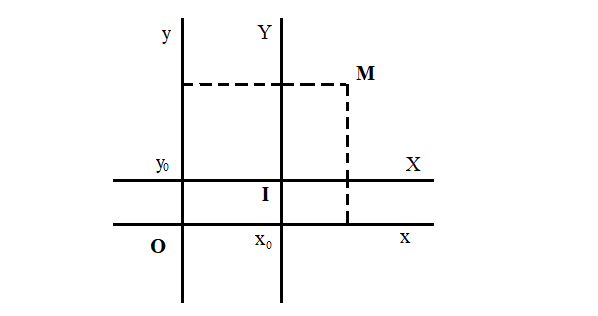
Chú ý: \(M(x,y)\in (C)\Leftrightarrow y=f(x)\)
\(\Leftrightarrow Y+y_{0}=f(X+x_{0})\Leftrightarrow Y=g(X)\)
2. Chứng minh đường thẳng \(\Delta : x=x_{0}\) là trục đối xứng của đồ thị (C) của hàm số y=f(x)
Đồ thị của hàm số chẵn luôn nhận trục tung là trục đối xứng. Vậy để chứng minh đường thẳng \(\Delta : x=x_{0}\) là trục đối xứng, ta dùng công thức đổi trục \(\left\{\begin{matrix} x=x_{0}+X & \\ y=Y & \end{matrix}\right.\) để đưa hệ số \(Oxy\) về hệ trục \(IXY\) (\(\Delta\) là trục tung) và chứng minh: trong hệ trục \(IXY\), hàm số đã cho có dạng \(Y=g(X)\) là hàm số chẵn.