Đề bài
Câu 1: Cho hình nón có tỉ lệ giữa bán kính đáy và đường sinh bằng \(\dfrac{1}{3}\). Hình cầu nội tiếp hình nón này có thể tích bằng V. Thể tích hình nón bằng.
A. 2V B. 4V
C. 5V D. 3V
Câu 2: Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. gọi S1là diện tích 6 mặt của hình lập phương, S2 là diện tích xung quanh của hình trụ. Hãy tính tỷ số \(\dfrac{{{S_1}}}{{{S_2}}}\) và chọn đáp án đúng:
\(A.\,\,\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{1}{2}\) \(B.\,\,\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{\pi }{6}\)
\(C.\,\,\dfrac{{{S_1}}}{{{S_2}}} = \pi \) \(D.\,\,\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{\pi }{2}\)
Câu 3: Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh đều bằng a. Diện tích của mặt cầu ngoại tiếp hình lăng trụ tính theo a bằng:
\(A.\,\,\dfrac{{7\pi {a^2}}}{3}\) \(B.\,\,\dfrac{{2\pi {a^2}}}{3}\)
\(C.\,\,\dfrac{{8\pi {a^2}}}{3}\) \(D.\,\,\dfrac{{5\pi {a^2}}}{3}\)
Câu 4: Một hình trụ có bán kính đáy r = 5cm và khoảng cách giữa hai đáy bằng 7cm. Khi đó thể tích của khối trụ được tạo nên là:
A. 459,77 cm3 B. 549,77 cm3
C. 594,77 cm3 D. 281,1 cm3
Câu 5: Trong các khẳng định sau, hãy lựa chọn khẳng định sai:
A. Có một mặt cầu đi qua các đỉnh của một hình tứ diện bất kỳ.
B. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.
C. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi
D. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật
Câu 6: Trong một chiếc hộp hình trụ, người ta bỏ vào đấy ba quả tennis, biết rằng đáy của hình trụ bằng hình tròn lớn trên quả banh và chiều cao của hình trụ bằng ba lần đường kính quả banh. gọi S1 là tổng diện tích của ba quả banh, S2 là diện tích xung quanh hình trụ. Tỷ số diện tích \(\dfrac{{{S_1}}}{{{S_2}}}\) là:
A. 5 B. 1
C. 4 D. 2
Câu 7: Một hình trụ có bán kính đáy r = 5 cm và khoảng cách giữa hai đáy bằng 7cm. Khi đó diện tích xung quanh của hình trụ là:
A. 219,91 cm2 B. 921,91 cm2
C. 19,91 cm2 D. 291,91 cm2
Câu 8: Cho hình lập phương ABCD. A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó \(\dfrac{{{V_{(H)}}}}{{{V_{ABCD.A'B'C'D'}}}}\) bằng:
\(A.\,\,\dfrac{\pi }{{\sqrt 3 }}\) \(B.\,\,\dfrac{\pi }{6}\)
\(C.\,\,\dfrac{\pi }{3}\) \(D.\,\,\dfrac{\pi }{4}\)
Câu 9: Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó \(\dfrac{{{V_{(H)}}}}{{{V_{ABCD.A'B'C'D'}}}}\) bằng:
\(A.\,\,\dfrac{\pi }{6}\) \(B.\,\,\dfrac{\pi }{{12}}\)
\(C.\,\,\dfrac{1}{3}\) \(D.\,\,\dfrac{\pi }{8}\)
Câu 10:
Cho tứ diện ABCD có AD⊥(ABC) và BD⊥BC. Khi quay tứ điện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành.
A. 2 B. 1
C. 4 D. 3
Lời giải chi tiết
| 1A | 2B | 3A | 4B | 5C |
| 6B | 7A | 8B | 9B | 10A |
Câu 1:
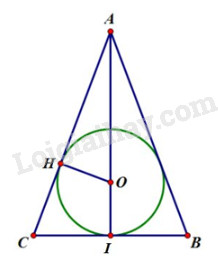
Gọi r và R lần lượt là bán kính của đường tròn đáy của hình nón và bán kính của mặt cầu nội tiếp hình nón.
Áp dụng định lí Pitago vào tam giác vuông AIC ta có:
\(AI = \sqrt {A{C^2} - I{C^2}} = \sqrt {{l^2} - {r^2}} \)\(\, = \sqrt {{{\left( {3r} \right)}^2} - {r^2}} = 2\sqrt 2 r\)
\(OA = AI - OI = 2\sqrt 2 r - R\)
\(\Delta OAH\) đồng dạng \(\Delta CAI\) (g.g)
\(\begin{array}{l} \Rightarrow \dfrac{{CI}}{{OH}} = \dfrac{{AC}}{{AO}} \Rightarrow \dfrac{r}{R} = \dfrac{{3r}}{{2\sqrt 2 r - R}}\\ \Rightarrow 3R = 2\sqrt 2 r - R \Rightarrow 4R = 2\sqrt 2 r\\ \Rightarrow r = \sqrt 2 R\end{array}\)
Thể tích của mặt cầu nội tiếp hình nón là: \(V = \dfrac{4}{3}\pi {R^3}\)
Thể tích của hình nón là:
\(V' = \dfrac{1}{3}\pi {r^2}.2\sqrt 2 r = \dfrac{1}{3}\pi .2\sqrt 2 .{\left( {\sqrt 2 R} \right)^3} \)\(\,= \dfrac{8}{3}\pi {R^3} = 2V\)
Chọn A
Câu 2:
Hình trụ có bán kính đáy \(\dfrac{a}{2}\) , chiều cao h = a
Suy ra: \({S_1} = 6{a^2};{S_2} = \pi {a^2}\)
Vậy \(\dfrac{{{S_2}}}{{{S_1}}} = \dfrac{\pi }{6}.\)
Chọn B
Câu 3:
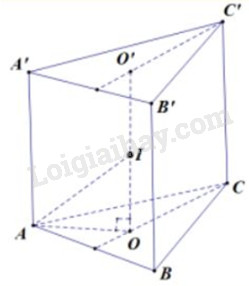
Gọi O và O’ lần lượt là tâm mặt cầu ngoại tiếp tam giác ABC và A’B’C’
Khi đó tâm mặt cầu (S) ngoại tiếp lăng trụ ABCA’B’C’ chính là trung điểm I của OO’
Mặt cầu này có bán kính là: \(R = IA = \sqrt {A{O^2} + O{I^2}} \)\(\, = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} \)\(\,= \dfrac{{a\sqrt {21} }}{6}\)
Diện tích mặt cầu là: \(S = 4\pi {R^2} = 4\pi {\left( {\dfrac{{a\sqrt {21} }}{6}} \right)^2} = \dfrac{{7\pi {a^2}}}{3}\)
Chọn A
Câu 4:
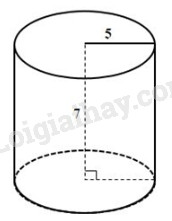
Thể tích của hình trụ là:
\(V = h.B = 7.\pi {5^2} = 549,77\,c{m^3}\)
Chọn B
Câu 5: Chọn C
Câu 6: Gọi R là bán kính 1 quả banh
\( \Rightarrow \) Tổng diên tích 3 quả banh là: \({S_1} = 3.4\pi {R^2} = 12\pi {R^2}\)
Chiếc hộp có bán kính đáy cũng bằng R và chiều cao bằng h = 6R
\( \Rightarrow \) Diện tích xung quanh hình trụ là: \({S_2} = 2\pi Rh = 12\pi {R^2}\)
\( \Rightarrow \dfrac{{{S_1}}}{{{S_2}}} = 1\)
Chọn B.
Câu 7:
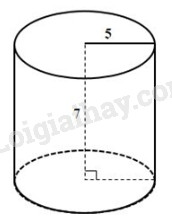
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi r.h = 2\pi .5.7 = 219,91\,c{m^2}\)
Chọn A.
Câu 8:
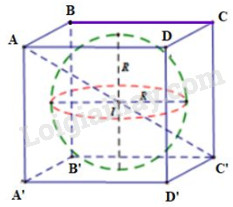
Mặt cầu nội tiếp hình lập phương cạnh a có bán kính bằng \(\dfrac{a}{2}\)
Thể tích mặt cầu nội tiếp hình lập phương là:
\({V_{(H)}} = \dfrac{4}{3}\pi {\left( {\dfrac{a}{2}} \right)^3} = \dfrac{{\pi {a^3}}}{6}\)
Tỉ số: \(\dfrac{{{V_{(H)}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{{\dfrac{{\pi {a^3}}}{6}}}{{{a^3}}} = \dfrac{\pi }{6}\)
Chọn B
Câu 9:
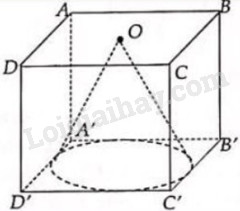
Khối nón có đỉnh là tâm hình vuông ABCD và đáy là đường tròn nội tiếp hình vuông A’B’C’D’ có bán kính đáy \(R = \dfrac{a}{2}\) , chiều cao \(h = a\)
Vậy thể tích khối nón là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {\dfrac{a}{2}} \right)^2}a = \dfrac{1}{{12}}\pi {a^3}.\)
Chọn B
Câu 10:
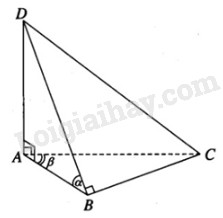
Tứ diện ABCD có \(\widehat {BAD} = {90^o}\) nên \(\widehat {ABD} = \alpha \) là một góc nhọn. Khi quay các cạnh của tứ diện đó xung quanh cạnh AB thì cạnh BD tạo thành một hình nón tròn xoay đỉnh B có trục là AB, cạnh AD vuông góc với AB tạo thành đáy của hình nón đó.
Mặt khác theo giả thiết ta có \(BD \bot BC\) nên\(AB \bot BC\) . Ta có \(\widehat {BAC} = \beta \) là một góc nhọn. Do đó khi quay các cạnh của tứ diện xung quanh cạnh AB thì cạnh AC tạo thành một hình nón tròn xoay đỉnh A có trục là AB, còn cạnh BC tạo thành đáy của hình nón.
Như vậy khi quay tất cả các cạnh của tứ diện xung quanh trục AB thì các cạnh BD và AC tạo thành hai hình nón.
Chọn A.

