Đề bài
Câu 1. Trong mặt phẳng tọa độ Oxy, cho điểm M là điểm biểu diễn cho số phức z = a + bi. Tính S = a + b.
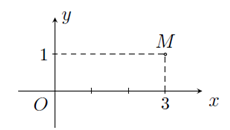
A. S = 4 B. S = 1
C. S = 2 D. S = 3.
Câu 2. Điểm nào trong các điểm sau đây là điểm biểu diễn hình học của số phức z = - 5 + 4i trong mặt phẳng tọa độ Oxy.
A. A(- 5 ; 4). B. B(5 ; - 4 ).
C. C(4 ; - 5). D. D(4 ; 5).
Câu 3. Trong C, phương trình z3+1=0 có nghiệm là :
A. S={−1;2±i√32}.
B. S={−1}.
C. S={−1;5±i√34}.
D. S={−1;1±i√32}.
Câu 4. Số phức z thỏa mãn |z|=5 và phần thực của z bằng hai lần phần ảo của nó.
A. [z=2√5+i√5z=−2√5−i√5.
B. [z=−2√5+i√5z=2√5−i√5.
C. [z=√5+2√5iz=−√5−2√5i.
D. [z=−√5+2√5iz=√5−2√5i.
Câu 5. Cho số phức z thỏa mãn |z−2−2i|=1. Tập hợp điểm biểu diễn số phức z – i trong mặt phằng tọa độ là đường tròn có phương trình :
A. (x−2)2+(y−1)2=1.
B. (x+2)2+(y−1)2=1.
C. (x−2)2+(y−2)2=1.
D. (x+2)2+(y+1)2=1
Câu 6. Điểm biểu diễn cùa các số phức z = 7 + bi với b∈R, nằm trên đường thẳng có phương trình là:
A. x = 7. B. y = 7.
C. y = x. D. y = x + 7.
Câu 7. Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z’ = - 2 +5i. Tìm mệnh đề đúng trong các mệnh để sau:
A. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x.
B. Hai điểm A và B đối xứng với nhau qua trục hoành.
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
D. Hai điểm A và B đối xứng với nhau qua trục tung.
Câu 8. Biết rằng số phức liên hợp của z là ¯z=(2+3i)+(4−8i). Tìm số phức z.
A. z=−6−5i.
B. z=6+5i.
C. z=−6+5i.
D. z=6−5i.
Câu 9. Cho ¯z=(5−2i)(−3+2i). Giá trị của 2|z|−5√377 bằng :
A. −10√377. B. 10√377.
C. 7√377. D. −3√377.
Câu 10. Tìm số phức z biết |z|=5 và phần thực lớn hơn phần ảo một đơn vị .
A. z1=3+4i,z2=−4−3i.
B. z1=4+3i,z2=−3−4i.
C. z1=−4−3i,z2=3+4i
D. z1=(2√3+1)+2√3 z2=(−2√3+1)−2√3i
Câu 11. Cho số phức z = a + bi và ¯z là số phức liên hợp của z. Chọn kết luận đúng.
A. z+¯z=2a. B. z.¯z=1.
C. z−¯z=2b. D. z.¯z=z2.
Câu 12. Cho các số phức z1=−1+i,z2=1−2i,z3=1+2i. Giá trị biểu thức T=|z1z2+z2z3+z3z1| là:
A. 1 B. √13
C. 5 D. 13
Câu 13. Cho hai số phức z1=3−2i z2=(a2+a+1)+(2a2+3a−4)i. Tìm a∈R để z1=z2.
A. a = -3. B. a = 1.
C. a = - 1 . D. a = - 2 .
Câu 14. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức 3−2√2i. Tìm a , b.
A. a = 3 , b = 2.
B. a = 3 , b = 2√2.
C. a = 3 , b = √2.
D. a = 3 , b = −2√2.
Câu 15. Tập hợp các điểm biểu diễn số phức z thỏa mãn |z−2i|=4 là:
A. Đường tròn tâm I(1 ; - 2), bán kính R = 4.
B. Đường tròn tâm I(1 ; 2), bán kính R = 4.
C. Đường tròn tâm I(0 ; 2), bán kính R = 4.
D. Đường tròn tâm I(0 ; -2), bán kính R = 4.
Câu 16. Xác định số phức z thỏa mãn |z−2−2i|=√2 mà |z| đạt giá trị lớn nhất.
A. z = 1 + i.
B. z = 3 + i.
C. z = 3 + 3i.
D. z = 1+ 3i.
Câu 17. Cho số phức z=r(cosπ4+isinπ4). Chọn 1 acgumn của z:
A. −π4 B. 5π4
C. 9π4 D. −5π4.
Câu 18. Cho số phức z=1+i2−i. Mô đun của z là:
A. √25. B. √52
C. 25 D. 52.
Câu 19. Số phức z có mô đun r = 2 và acgumen φ=−π2 thì có dạng lượng giác là:
A. z=2(cos(−π2)+isin(−π2)).
B. z=2(cos(−π2)−isin(−π2)).
C. z=2(cos(π2)+isin(π2)).
D. z=2(−cos(−π2)+isin(−π2)).
Câu 20. Phương trình z2+az+b=0 nhận z = 1 – 2i làm nghiệm Khi đó a + b bằng:
A. 3 B. 4
C. 5 D. 6.
Câu 21. Gọi số phức z có dạng đại số và dạng lượng giác lần lượt là z = a + bi và z=r(cosφ+isinφ). Chọn mệnh đề đúng .
A. r=√a2+b2.
B. r=a2+b2.
C. r2=√a2+b2.
D. r=|a+b|.
Câu 22. Cho số phức z có dạng lượng giác z=2(cosπ2+isinπ2). Dạng lượng giác của z là:
A. z = 2.
B. z = 2i.
C. z = -2 .
D. z = - 2i.
Câu 23. Trong mặt phẳng phức, A, B, C lần lượt là các điểm biểu diễn của các số phức z1=1+2i,z2=2+3i,z3=3+4i. Trọng tâm tam giác ABC là điểm :
A. G ( 2 ; -3 ).
B. G (2 ; 3).
C. G ( 3 ; 2).
D. G (-3 ;2).
Câu 24. Cho số phức z = 4 + 3i. Tìm phần thực và phần ảo của z.
A. Phần thực của z là 4, phần ảo của z là 3.
B. Phần thực của z là 4, phần ảo của z là 3i.
C. Phần thực của z là 3, phần ảo của z là 4.
D. Phần thực của z là 3, phần ảo của z là 4i.
Câu 25. Tổng của hai số phức z1=2+3i,z2=5−6ilà:
A. 7 – 3i.
B. 7 + 3i.
C. – 3 +9i.
D. 3 + 9i.
Lời giải chi tiết
| 1 | 2 | 3 | 4 | 5 |
| A | A | D | A | A |
| 6 | 7 | 8 | 9 | 10 |
| A | D | B | D | B |
| 11 | 12 | 13 | 14 | 15 |
| A | B | D | D | C |
| 16 | 17 | 18 | 19 | 20 |
| C | C | A | A | A |
| 21 | 22 | 23 | 24 | 25 |
| A | B | B | A | A |
Lời giải chi tiết
Câu 1: A
Câu 2: A
Câu 3: D
z3+1=0⇔(z+1)(z2−z+1)=0⇔[z+1=0(1)z2−z+1=0(2)
(1)⇔z=−1
Giải (2):
Δ=b2−4ac=1−4=−3=3i2
⇒Δcó hai căn bậc hai là i√3và −i√3
⇒Phương trình có hai nghiệm: z1=1+i√32,z2=1−√32
Câu 4: A
Đặt z= x+ yi x,y∈Z
Theo yêu cầu bài toán ta có:
{|z|=5x=2y⇔{|x+yi|=5x=2y⇔{√x2+y2=5(1)x=2y(2)
Thay (2) vào (1), ta được:
√4y2+y2=5⇔5y2=25⇔y2=5⇔[y=√5⇒x=2√5y=−√5⇒x=−2√5
⇒z=2√5+i√5
⇒z=−2√5−i√5
Câu 5: A
Đặt z−i=x+yi
⇒z=x+(y+1)i|z−2−2i|=1⇒|x+(y+1)i|=1⇔|(x−2)+(y−1)i|=1⇔√(x−2)2+(y−1)2=1⇔(x−2)2+(y−1)2=1
⇒ Tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ là đường tròn có phương trình:(x−2)2+(y−1)2=1
Câu 6: A
Câu 7: D
Câu 8: B
Câu 9: D
Ta có: ¯z= (5−2i)(−3+2i)= −15−4i2+6i+10i=−11+16i
Câu 10: B
Đặt z=x+yix,y∈Z
Theo đề bài ta có:
{|z|=5x=y+1⇔{|x+yi|=5x=y+1⇔{√x2+y2=5(1)x=y+1(2)(1)(2)
Thay( 2) vào (1) ta được:
√(y+1)2+y2=5⇔2y2+2y−24=0⇔[y=3⇒x=4⇒z=4+3iy=−4⇒x=−3⇒z=−3−4i
Câu 11: A
Câu 12: B
z1=−1+i , z2=1−2i , z3=1+2i
z1z2+z2z3+z3z1=(−1+i)(1−2i)+(1−2i)(1+2i)+(1+2i)(−1+i)=(−1+i)[(1−2i)+(1−2i)]+(1−2i)(1+2i)=(−1+i)2+1−4i2=−2+2i+5=3+2i
Câu 13: D
z1=z2⇔3−2i=(a2+a+1)+(2a2+3a−4)⇔{a2+a+1=32a2+3a−4=−2⇔{a2+a−2=02a2+3a−2=0⇔{a2+a=2(1)2a2+3a−2=0(2)
Thay (1) vào (2) được:
4+a−2=0⇔a=−2
Câu 14: D
Câu 15: C
Đặt z=x+yi
|z−2i|=4⇒|x+yi−2i|=4⇔|x+(y−2)i|=4⇔√x2+(y−2)2=√2
⇒Tập hợp điểm biểu diễn M(x,y) biểu diễn số phức là đường tròn tâm I(2,2) , bán kính =√2
Có |z|=|x+yi|=√x2+y2
Lấy O(0,0); M(x,y)
⇒OM=√x2+y2
Do M chạy trên đường tròn, Ocố định nênMO lớn nhất khi Mlà giao điểm của OIvới đường tròn
Có O(0,0), I(2,2) nên →OI=(2,2)
Phương trình đường thẳng OI: {x=2ty=2t (1)
Mặt khác: OI là giao với đường tròn tại M nên thay (1) vào phương trình đường tròn ta được:
(2t−2)2+(2t−2)2=2⇔(2t−2)2=1⇔[2t−2=12t−2=−1⇔[z=32⇒M1(3,3)⇒OM1=3√2z=12⇒M2(1,1)⇒OM2=√2
⇒zmax với M(3,3)
\Rightarrow z = 3 + 3i
Câu 17: C
Câu 18: A
\begin{array}{l}z = \dfrac{{1 + i}}{{2 - i}} = \dfrac{{(1 + i)(2 - i)}}{{4 - {i^2}}}\\\,\,\,\, = \dfrac{{2 - {i^2} + 2i - i}}{5}\\\,\,\,\, = \dfrac{{3 + i}}{5} = \dfrac{3}{5} + \dfrac{1}{5}i\end{array}
\Rightarrow \left| z \right| = \sqrt {\dfrac{9}{{25}} + \dfrac{1}{{25}}} = \dfrac{{\sqrt {10} }}{5} = \sqrt {\dfrac{2}{5}}
Câu 19: A
Câu 20: A
Phương trình {z^2} + az + b = 0 nhận {z_1} = 1 - 2i \to nghiệm còn lại là {z_2} = 1 + 2i
Theo Vi- et ta có:
\begin{array}{l}y' = 0 \Leftrightarrow 4(m + 1){x^3} - 2mx = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{2m}}{{4m + 4}}{\rm{ (1)}}\end{array} \right.\\y = (m + 1){x^4} - m{x^2} + 3\\\dfrac{{2m}}{{4m + 4}} > 0 \Leftrightarrow \left[ \begin{array}{l}m > 0\\m < - 1\end{array} \right. \\ \Rightarrow m \in \left( { - \infty , - 1} \right) \cup \left( {0, + \infty } \right)\end{array}
\Rightarrow a + b = 3
Câu 21: A
Câu 22: B
Câu 23: B
\begin{array}{l}{z_1} = 1 + 2i \to A(1,2)\\{z_2} = 2 + 3i \to B(2,3)\\{z_3} = 3 + 4i \to C(3,4)\\\end{array}
\Rightarrow Trọng tâm tam giác ABC: G(2,3)
Câu 24:A
Câu 25: A
{z_1} + {z_2} = 2 + 3i + 5 - 6i = 7 - 3i
