Video hướng dẫn giải
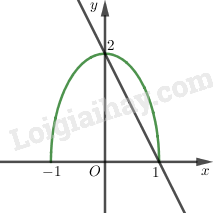
Xét hình phẳng D giới hạn bởi \(y = 2\sqrt {1 - {x^2}} \) và \(y = 2(1-x)\)
LG a
a) Tính diện tích hình D
Phương pháp giải:
+) Hình phẳng được giới hạn bởi đường các đồ thị hàm số \(y=f(x);\) \(y=g(x)\) và các đường thẳng \(x=a; \, \, x=b \, (a<b)\) có diện tích được tính bởi công thức: \(S = \displaystyle \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \)
Lời giải chi tiết:
Phương trình hoành độ giao điểm của hai đồ thị là:
\(\eqalign{
& 2\sqrt {1 - {x^2}} = 2(1 - x) \Leftrightarrow \left\{ \matrix{
1 - x \ge 0 \hfill \cr
1 - {x^2} = {(1 - x)^2} \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x \le 1 \hfill \cr
2{x^2} - 2x = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \le 1 \hfill \cr
\left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \cr} \)
Đồ thị của hàm số \(y = 2\sqrt {1 - {x^2}} \) là một nửa elip \({x^2} + \dfrac {y^2} 4 = 1\) với \(y ≥ 0.\)
Từ đồ thị trên ta có, diện tích của D:
\(\eqalign{
& S = \int_0^1 {\left[ {2\sqrt {1 - {x^2}} - 2(1 - x)} \right]} dx \cr
& = 2\left[ {\int_0^1 {\sqrt {1 - {x^2}} dx - \int_0^1 {(1 - x)dx} } } \right] \cr} \)
Tính \(\displaystyle \int_0^1 {\sqrt {1 - {x^2}} } dx\):
Đặt \(x = \sin t\) , ta có: \(dx = \cos t dt\); \(x=0 \Rightarrow t= 0\); \(x=1 \Rightarrow t={\pi \over 2}\)
Suy ra:
\(\eqalign{
& \int_0^1 {\sqrt {1 - {x^2}} } dx = \int_0^{{\pi \over 2}} {\sqrt {1 - {{\sin }^2}t} } .\cos tdt \cr
& = \int_0^{{\pi \over 2}} {{\mathop{\rm \cos t}\nolimits} .\cos tdt = \int_0^{{\pi \over 2}} {{{\cos }^2}tdt} } \cr
& = {1 \over 2}\int_0^{{\pi \over 2}} {(1 + \cos 2t)dt = {1 \over 2}} \left[ {t + {1 \over 2}\sin 2t} \right]\left| {_0^{{\pi \over 2}}} \right. = {\pi \over 4} \cr
& = \int\limits_0^1 {(1 - x)dx} = \left. {\left( {x - \frac{{{x^2}}}{2}} \right)} \right|_0^1 = \frac{1}{2} \cr
& \Rightarrow D = 2\left({\pi \over 4} - {1 \over 2}\right) = {\pi \over 2}-1 \cr} \)
LG b
b) Quay hình D xung quanh trục \(Ox\). Tính thể tích khối tròn xoay được tạo thành.
Phương pháp giải:
+) Thể tích khối tròn xoay có được khi quay hình phẳng D giới hạn bởi các đường \(x=a,x=b,y=f(x),y=g(x)\) quanh \(Ox\) là \(V = \pi \displaystyle\int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Dựa vào hình trên ta có thể tích cần tìm là:
\(\begin{array}{l}
V = \pi \displaystyle\int\limits_0^1 {\left[ {{{\left( {2\sqrt {1 - {x^2}} } \right)}^2} - {{\left( {2\left( {1 - x} \right)} \right)}^2}} \right]dx} \\
= \pi \displaystyle\int\limits_0^1 {\left[ {4\left( {1 - {x^2}} \right) - 4{{\left( {1 - x} \right)}^2}} \right]dx}
\end{array}\)
\(\eqalign{
&= 4\pi \displaystyle\int_0^1 {\left[ {(1 - {x^2}) - (1 - {x})^2} \right]} dx \cr
& = 8\pi \displaystyle\left. {\left( {\frac{{{x^2}}}{2} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 \cr
& = 8\pi \left({1 \over 2} - {1 \over 3}\right) = {{4\pi } \over 3} \, \, (đvdt). \cr} \)