Đề bài
Tính thể tích khối bát diện đều cạnh \(a\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Chia khối bát diện đều thành hai khối chóp tứ giác đều.
+) Xác định chiều cao và áp dụng công thức tính thể tích khối chóp: \(V = \dfrac{1}{3}h.{S_d}\)
Lời giải chi tiết
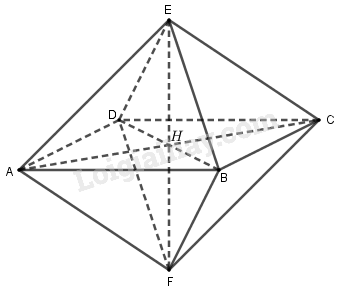
Chia khối tám mặt đều cạnh \(a\) thành hai khối chóp tứ giác đều cạnh \(a\) là \(E.ABCD\) và \(F.ABCD\).
Xét chóp tứ giác đều \(E.ABCD\). Gọi \(H\) là tâm hình vuông \(ABCD\) ta có: \(EH \bot \left( {ABCD} \right)\).
Vì \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = \sqrt {A{B^2} + B{C^2}} \) \(= \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AH = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\).
Áp dụng định lí Pitago trong tam giác vuông \(EHA\) có: \(E{H^2} = E{A^2} - A{H^2} \) \(= {a^2} - {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} \)\( = \dfrac{{{a^2}}}{2}\)
\(\Rightarrow EH = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow {V_{E.ABCD}} = \dfrac{1}{3}EH.{S_{ABCD}} \) \(= \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Vậy thể tích khối tám mặt đều cạnh \(a\) là: \(V = 2.{V_{E.ABCD}}= \displaystyle {{{a^3} \sqrt 2 } \over 3}\).
Chú ý: Hình chóp đa giác đều có hình chiếu của đỉnh trên mặt đáy trùng với tâm mặt đáy.