Video hướng dẫn giải
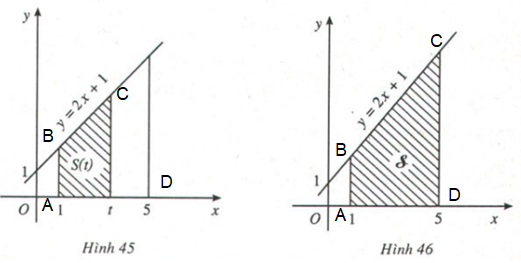
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng \(y = 2x + 1\), trục hoành và hai đường thẳng \(x = 1, x = t\) \((1 \le t \le 5)\) (H.45).
LG a
Tính diện tích \(S\) của hình \(T\) khi \(t = 5 \) (H.46).
Phương pháp giải:
Dựa vào công thức tính diện tích hình thang \(ABCD (AB//CD)\) là:\(S = \dfrac{{\left( {AB + CD} \right).h}}{2}\)
Lời giải chi tiết:
(Hình 46)
Kí hiệu \(A\) là điểm có tọa độ \((1,0), D\) là điểm có tọa độ \((5,0)\). \(B, C\) lần lượt là giao điểm của đường thẳng \(x = 1\) và \(x = 5\) với đường thẳng \(y = 2x + 1\).
- Khi đó \(B\) và \(C\) sẽ có tọa độ lần lượt là \((1,3)\) và \((5,11)\).
- Ta có: \(AB = 3, CD = 11, AD = 4\). Diện tích hình thang:
\(\displaystyle ABCD = {{(AB + CD).AD} \over 2} = 28\)
LG b
Tính diện tích \(S(t)\) của hình \(T\) khi \(x ∈ [1; 5]\).
Phương pháp giải:
Dựa vào công thức tính diện tích hình thang \(ABCD (AB//CD)\) là:\(S = \dfrac{{\left( {AB + CD} \right).h}}{2}\)
Lời giải chi tiết:
Kí hiệu \(A\) là điểm có tọa độ \((1,0)\), \(D\) là điểm có tọa độ \((t,0)\). B, C\) lần lượt là giao điểm của đường thẳng \(x = 1\) và \(x = t\) với đường thẳng \(y = 2x + 1\).
- Khi đó ta có \(B (1,3)\) và \(C(t, 2t + 1)\).
- Ta có \(AB = 3, AD = t – 1, CD = 2t + 1\).
- Khi đó diện tích hình thang:
\(\displaystyle S(t) = {{(AB + CD).AD} \over 2} \) \(\displaystyle= {{(3 + 2t + 1).(t - 1)} \over 2} \) \(= {t^2} + t - 2\)
Do đó \(S(t)= {t^2} + t - 2\)
LG c
Chứng minh rằng \(S(t)\) là một nguyên hàm của \(f(t)=2t+1, t\in [1;5]\) và diện tích \(S=S(5)-S(1)\).
Phương pháp giải:
Dựa vào công thức tính diện tích hình thang \(ABCD (AB//CD)\) là:\(S = \dfrac{{\left( {AB + CD} \right).h}}{2}\)
Lời giải chi tiết:
Vì \(S'(t)= ({t^2} + t - 2)'\) \(=2t+1\) nên hàm số \(S(t)\) là một nguyên hàm của hàm số \(f(t)=2t+1, t\in [1;5]\).
Dễ thấy \(S(5)-S(1)\) \(=\left( {{5^2} + 5 - 2} \right) - \left( {{1^2} + 1 - 2} \right) \) \(= 28 = S\) hay \(S=S(5)-S(1)\).