Video hướng dẫn giải
Trong mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện:
LG a
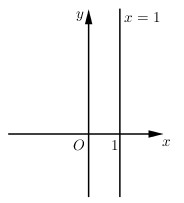
a) phần thực của \(z\) bằng \(1\)
Phương pháp giải:
Điểm \(M\left( {x;y} \right)\) trên mặt phẳng tọa độ \(Oxy\) là điểm biểu diễn cho số phức \(z=x+yi\).
Tìm điều kiện của \(x;y\) và biểu diễn tập hợp điểm M trên mặt phẳng tọa độ.
Lời giải chi tiết:
Ta có \(x = 1, y\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(x = 1\).
LG b
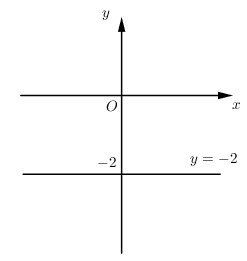
b) phần ảo của \(z\) bằng \(-2\)
Lời giải chi tiết:
Ta có \(y = -2, x\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(y = -2\).
LG c
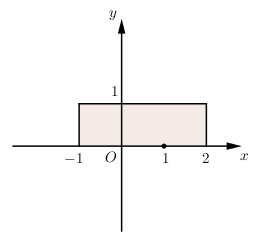
c) Phần thực của \(z\) thuộc đoạn \([-1, 2]\), phần ảo của \(z\) thuộc đoạn \([0, 1]\)
Lời giải chi tiết:
Ta có \(x \in \left[ { - 1;2} \right]\), tức là \( - 1 \le x \le 2\), tập hợp các điểm M nằm bên trái đường thẳng \(x=2\) và nằm bên phải đường thẳng \(x=-1\) và \(y ∈ [0, 1]\), tức là \(0 \le y \le 1\) tập hợp các điểm M nằm bên dưới đường thẳng \(y=1\) và nằm bên trên đường thẳng \(y=0\).
Vậy tập hợp các điểm biểu diễn \(z\) là hình chữ được tô màu.
LG d
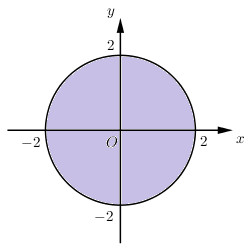
d) \(|z| ≤ 2\)
Lời giải chi tiết:
Ta có:
\(\left| z \right| \le 2 \Leftrightarrow \sqrt {{x^2} + {y^2}} \le 2 \Leftrightarrow {x^2} + {y^2} \le 4\)
Vậy tập hợp các điểm biểu diễn \(z\) là hình tròn tâm \(O\) (gốc tọa độ) bán kính bằng \(2\) (kể cả các điểm trên đường tròn).