Video hướng dẫn giải
LG a
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
y=−x4+8x2−1y=−x4+8x2−1;
Phương pháp giải:
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
Bước 1: Tìm TXĐ của hàm số.
Bước 2: Khảo sát sự biến thiên:
*) Xét chiều biến thiên của hàm số:
+) Tính đạo hàm.
+) Tìm các điểm xixi mà tại đó đạo hàm có y′=0 hoặc đạo hàm không xác định.
+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
*) Tìm cực trị: y(xi).
*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số nếu có: limx→±∞y;limx→x0y...
*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
Bước 3: Đồ thị:
+) Giao điểm của đồ thị với trục tung: x=0⇒y=....⇒A(0; .....).
+) Giao điểm của đồ thị với trục hoành: y=0⇒x=.....⇒B(...;0).
+) Các điểm cực đại, cực tiểu nếu có.
Lời giải chi tiết:
Tập xác định: D=R;
Sự biến thiên:
Ta có: y′=−4x3+16x=−4x(x2−4)
⇒y′=0⇔−4x(x2−4)=0 ⇔[x=0x2−4=0⇔[x=0x=±2
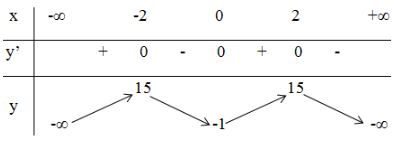
- Hàm số đồng biến trên khoảng (−∞;−2) và (0;2); nghịch biến trên khoảng (−2;0) và 2;+∞).
- Cực trị:
Hàm số đạt cực đạt tại hai điểm x=−2 và x=2; yCĐ=y(±2)=15.
Hàm số đạt cực tiểu tại x=0; yCT=−1
- Giới hạn: limyx→±∞=−∞
Bảng biến thiên:
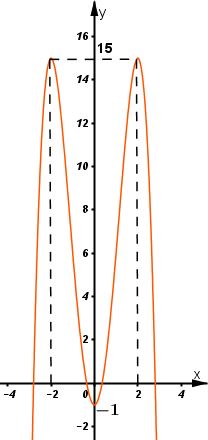
Đồ thị giao Oy tại điểm (0;−1)
Hàm số đã cho là hàm số chẵn nhận trục Oy làm trục đối xứng.
Đồ thị
LG b
y=x4−2x2+2;
Lời giải chi tiết:
Tập xác định: D=R;
Sự biến thiên:
Ta có: y′=4x3−4x=4x(x2−1);
⇒y′=0⇔4x(x2−1)=0 ⇔[x=0x2−1=0⇔[x=0x=±1.
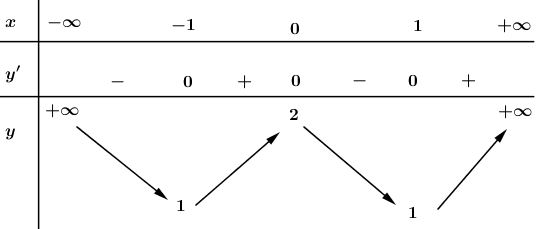
- Hàm số đồng biến trên khoảng (−1;0) và (1;+∞); nghịch biến trên khoảng (−∞;−1) và (0;1).
- Cực trị:
Hàm số đạt cực đại tại x=0; yCĐ=2.
Hàm số đạt cực tiểu tại hai điểm x=−1 và x=1; yCT=y(±1)=1.
-Giới hạn:
limyx→±∞=+∞
Bảng biến thiên:
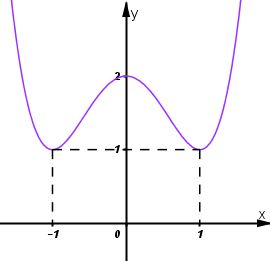
Hàm số đã cho là hàm số chẵn nhận trục Oy làm trục đối xứng.
Đồ thị giao Oy tại điểm (0;2)
Đồ thị
LG c
y=12x4+x2−32;
Lời giải chi tiết:
Tập xác định: D=R;
Sự biến thiên:
Ta có: y′=2x3+2x=2x(x2+1);
⇒y′=0⇔2x(x2+1)=0 ⇔[x=0x2+1=0⇔x=0.
- Hàm số nghịch biến trên khoảng (−∞;0); đồng biến trên khoảng (0;+∞).
-Cực trị:
Hàm số đạt cực tiểu tại x=0; yCT=−32
-Giới hạn:
limyx→±∞=+∞
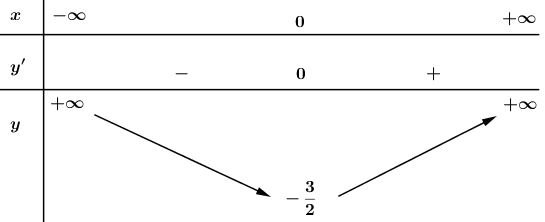
Bảng biến thiên :
Hàm số đã cho là hàm số chẵn, nhận trục Oy làm trục đối xứng.
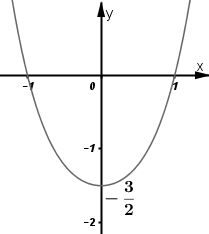
Đồ thị giao Ox tại hai điểm (−1;0) và (1;0); giao Oy tại (0;−32).
Đồ thị như hình bên.
LG d
y=−2x2−x4+3.
Lời giải chi tiết:
Tập xác định: D=R;
Sự biến thiên:
Ta có: y′=−4x−4x3=−4x(1+x2);
⇒y′=0⇔−4x(1+x2)=0 ⇔[x=0x2+1=0⇔x=0.
- Hàm số đồng biến trên khoảng: (−∞;0); nghịch biến trên khoảng: (0;+∞).
- Cực trị: Hàm số đạt cực đạt tại x=0; yCĐ=3.
- Giới hạn:
limyx→±∞=−∞
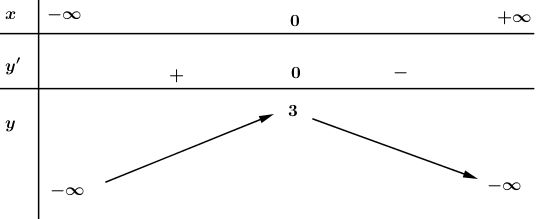
Bảng biến thiên:
Hàm số đã cho là hàm chẵn, nhận trục Oy làm trục đối xứng.
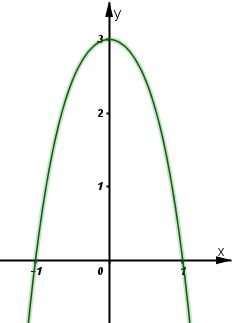
Đồ thị giao Ox tại hai điểm (1;0) và (−1;0); giao Oy tại điểm (0;3).
Đồ thị như hình bên.
