Đề bài
I. PHẦN TRẮC NGHIỆM(3 điểm)
Câu 1. Đồ thị hàm số \(y = {x^3} - 3{{\rm{x}}^2} + 2\) đi qua điểm nào?
A. \(M\left( { - 1;4} \right)\) B. \(N\left( {0; - 2} \right)\)
C. \(P\left( {1;0} \right)\) D. \(Q\left( {2;2} \right)\)
Câu 2. Hình chóp tứ giác có mấy mặt?
A. 4 B. 8 C. 5 D. 6
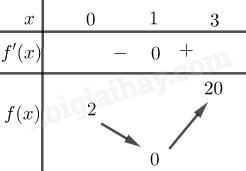
Câu 3. Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có bảng biến thiên như hình bên dưới.
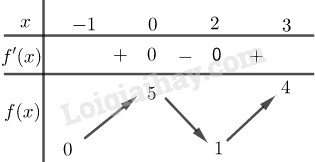
Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số không có cực trị.
B. Hàm số đạt cực đại tại \(x = 0\).
C. Hàm số đạt cực đại tại \(x = 5\).
D. Hàm số đạt cực đại tại \(x = 1\)
Câu 4. Thể tích V của khối chóp có diện tích đáy bằng B và chiều cao bằng h, được tính theo công thức
A. \(V = \dfrac{1}{4}Bh\). B. \(V = \dfrac{1}{2}Bh\)
C. \(V = Bh\) D. \(V = \dfrac{1}{3}Bh\)
Câu 5. Khối lăng trụ có diện tích đáy bằng 4, chiều cao bằng 3 có thể tích bằng
A. 12 B. 6 C. 4 D. 8
Câu 6. Đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) có phương trình là
A. \(y = 2\) B. \(x = 1\) C. \(x = 2\) D. \(y = 1\)
Câu 7. Đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) có phương trình là
A. \(y = 2\) B. \(x = 1\) C. \(x = 2\) D. \(y = 1\)
Câu 8. Khối lập phương cạnh bằng 2 có thể tích bằng
A. 4 B. 2 C. 8 D. 16
Câu 9. Hàm số \(y = \dfrac{{3 - 2x}}{{x + 7}}\) nghịch biến trên khoảng nào sau đây?
A. \(\left( { - \infty ;\dfrac{3}{2}} \right)\) B. \(\left( { - \infty ; + \infty } \right)\)
C. \(\left( { - \infty ; - 7} \right)\) D. \(\left( { - 8; + \infty } \right)\)
Câu 10. Hàm số \({x^4} + 2{x^2} - 3\) có bao nhiêu điểm cực trị?
A. 1 B. 3 C. 0 D. 2
Câu 11. Cho hàm số \(y = f\left( x \right) = {x^2} - 2x + 3\). Mệnh đề nào sau đây đúng?
A. \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 3\) B. \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 2\)
C. \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 6\) D. \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 0\)
Câu 12. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào?
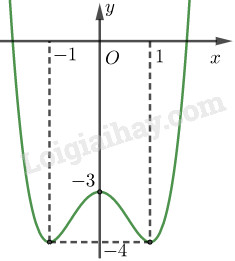
A. \(y = {x^4} + 2{x^2} - 3\) B. \(y = {x^4} - 2{x^2} - 3\)
C. \(y = - {x^4} - 2{x^2} + 3\) D. \(y = - {x^4} + 2{x^2} + 3\)
II. PHẦN TỰ LUẬN (7 điểm)
Câu 13.(3 điểm)
Cho hàm số \(y = {x^4} - 3x + 2\)
a) Tìm các khoảng đồng biến, nghịch biến của hàm số.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;3} \right]\)
Câu 14.(2,5 điểm)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với mặt phẳng (ABC), SA=AB=a.
a) Tính thể tích khối chóp S.ABC theo a.
b) Gọi M, N lần lượt là trung điểm của SB và BC. Tính thể tích của khối chóp A.SMNC theo a.
Câu 15.(1,5 điểm)
a) Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ.
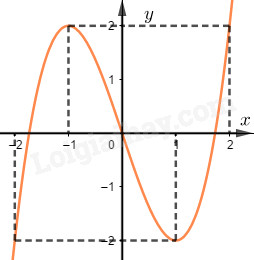
Hỏi phương trình \(\left| {f\left( x \right)} \right| = 2\) có bao nhiêu nghiệm?
b) Cho hàm số \(y = \dfrac{{x - 1}}{{{x^2} - 3{\rm{x}} + m}}\) có đồ thị là \(\left( C \right)\). Tìm tất cả các giá trị của tham số m để tổng số đường tiệm cận đứng và tiệm cận ngang của \(\left( C \right)\) bằng 2.
Lời giải chi tiết
PHẦN 1. TRẮC NGHIỆM
| 1.C | 2.C | 3. B | 4. D | 5. A | 6. C |
| 7. D | 8. C | 9. C | 10. A | 11. B | 12. B |
Câu 1. (TH)
Phương pháp
Thay tọa độ các điểm vào phương trình \(y = f\left( x \right)\)
Cách giải
Có \({1^3} - {3.1^2} + 2 = 0\)\( \Rightarrow P\left( {1;0} \right)\) thuộc đồ thị hàm số \(y = f\left( x \right)\).
Câu 2.(NB)
Phương pháp
Hình chóp n-giác có \(n + 1\) mặt.
Cách giải
Hình chóp tứ giác có 5 mặt
Câu 3. (NB)
Phương pháp
Hàm f đổi dấu từ dương sang âm qua \({x_0}\) thì đạt cực đại tại \({x_0}\)
Hàm f đổi dấu từ âm sang dương qua \({x_0}\) thì đạt cực tiểu tại \({x_0}\)
Cách giải
Hàm f đổi dấu từ dương sang âm qua \(x = 0\) thì đạt cực đại tại \(x = 0\).
Câu 4. (NB)
Phương pháp
Công thức thể tích hình chóp có diện tích đáy B, chiều cao h là: \(V = \dfrac{1}{3}B.h\)
Cách giải
Thể tích hình chóp có diện tích đáy B, chiều cao h là: \(V = \dfrac{1}{3}B.h\)
Câu 5. (TH)
Phương pháp
Công thức thể tích hình lăng trụ có diện tích đáy B, chiều cao h là: \(V = B.h\)
Cách giải
Thể tích hình chóp có diện tích đáy bằng 4, chiều cao bằng 3 là: \(V = 4.3 = 12\)
Câu 6. (TH)
Phương pháp
Đường thẳng \(x = {x_0}\) được gọi là tiệm cận đứng nếu ít nhất một trong các điều kiện sau được thỏa mãn \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = + \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = + \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = - \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = - \infty \).
Cách giải
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{x + 1}}{{x - 2}} = + \infty \)
Tiệm cận đứng của hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) là \(x = 2\)
Câu 7. (TH)
Phương pháp
Đường thẳng \(y = {y_0}\) được gọi là tiệm cận ngang nếu ít nhất một trong các điều kiện sau được thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0},\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).
Cách giải
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + 1}}{{x - 2}} = 1\)\( \Rightarrow y = 1\) là đường tiệm cận ngang.
Câu 8. (TH)
Phương pháp
Thể tích hình lập phương cạnh a: \(V = {a^3}\)
Cách giải
Thể tích lập phương cạnh 2 là: \(V = 8\)
Câu 9. Hàm số \(y = \dfrac{{3 - 2x}}{{x + 7}}\) nghịch biến trên khoảng nào sau đây?
A. \(\left( { - \infty ;\dfrac{3}{2}} \right)\) B. \(\left( { - \infty ; + \infty } \right)\)
C. \(\left( { - \infty ; - 7} \right)\) D. \(\left( { - 8; + \infty } \right)\)
Phương pháp
- Tìm tập xác định.
- Tính y’.
- Nếu \(y' > 0\forall x \in A\)\( \Rightarrow \) hàm số đồng biến trên A.
- Nếu \(y' < 0\forall x \in A\)\( \Rightarrow \) hàm số nghịch biến trên A.
Cách giải
Tập xác định: \(D = \mathbb{R}{\rm{\backslash }}\left\{ { - 7} \right\}\).
\(\begin{array}{l}y' = \dfrac{{ - 2\left( {x + 7} \right) - \left( {3 - 2x} \right)}}{{{{\left( {x + 7} \right)}^2}}}\\ = \dfrac{{ - 17}}{{{{\left( {x + 7} \right)}^2}}} < 0\forall x \in D\end{array}\)
\( \Rightarrow \)Hàm số nghịch biến trên \(\left( { - \infty ; - 7} \right)\) và \(\left( { - 7; + \infty } \right)\)
Câu 10. (TH)
Phương pháp
- Tính y’.
- Giải phương trình y’=0.
- Lập bảng biến thiên. Số cực trị bằng số điểm mà tại đó \(f'(x)\) đổi dấu.
Cách giải
\(y' = 4{x^3} + 4x = 4x\left( {{x^2} + 1} \right)\)
\(y' = 0 \Leftrightarrow x = 0\)
Bảng biến thiên:
\( \Rightarrow \) Hàm số có 1 điểm cực trị.
Câu 11. (VD)
Phương pháp
Bước 1: Tính y’.
Bước 2: Giải phương trình \(y' = 0\) tìm nghiệm \(x \in \left[ {0;3} \right]\). Tính giá trị của hàm số tại các nghiệm vừa tìm được và f(0), f(3).
Bước 3: So sánh các giá trị vừa tìm được ở bước 2, số lớn nhất trong các giá trị đó là GTLN, số nhỏ nhất là GTNN trên đoạn \(\left[ {0;3} \right]\)
Cách giải
Ta có \(y' = 2x - 2\)
\(y' = 0 \Leftrightarrow x = 1 \in \left[ {0;3} \right]\)
\(f\left( 0 \right) = 3,f\left( 3 \right) = 6\)
\(\mathop {\min }\limits_{\left[ {0;3} \right]} y = f\left( 1 \right) = 2\)
Câu 12.(NB)
Phương pháp
Quan sát dáng đồ thị để xác định hàm số là hàm trùng phương.
Từ đồ thị :
Nếu \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) thì hàm số có \(a > 0\).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) thì hàm số có \(a < 0\).
Tìm cực trị của hàm số để loại các đáp án sai.
Cách giải
Đồ thị trên là đồ thị của hàm số trùng phương.
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \Rightarrow a > 0\). \( \Rightarrow \)C, D sai.
Hàm số có các điểm cực trị là: \(x = 0;x = \pm 1\). \( \Rightarrow \)A sai.
II. PHẦN TỰ LUẬN (7 điểm)
Câu 13.(VD)
Cho hàm số \(y = {x^3} - 3x + 2\)
a) Tìm các khoảng đồng biến, nghịch biến của hàm số.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;3} \right]\)
Phương pháp
a)
Tìm tập xác định của hàm số.
Quan sát dấu \(y' > 0\) hay \(y' < 0\).
Nếu \(y' > 0\) trên khoảng \(\left( {a;b} \right)\) thì hàm số đồng biến trên khoảng \(\left( {a;b} \right)\).
Nếu \(y' < 0\) trên khoảng \(\left( {a;b} \right)\) thì hàm số nghịch biến trên khoảng \(\left( {a;b} \right)\).
b)
Bước 1: Giải phương trình \(y' = 0\) tìm nghiệm \(x \in \left[ {0;3} \right]\). Tính giá trị của hàm số tại các nghiệm vừa tìm được và f(0), f(3).
Bước 2: Quan sát bảng biến thiên, xác định giá trị điểm cao nhất và giá trị điểm thấp nhất của hàm số thông qua chiều biến thiên. Từ đó tìm GTLN, GTNN.
Cách giải
a) TXĐ:\(D = \mathbb{R}\)
\(y' = 3{x^2} - 3\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Bảng biến thiên:
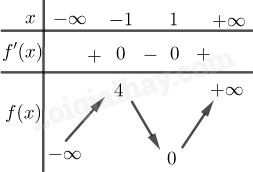
Từ bảng biến thiên ta có hàm số đồng biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\), nghịch biến trên \(\left( { - 1;1} \right)\).
b)
\(f\left( 0 \right) = 2\),\(f\left( 3 \right) = 20\),\(f\left( 1 \right) = 0\)
Từ bảng biến thiên ta có:
\( \Rightarrow \mathop {\min }\limits_{\left[ {0;3} \right]} y = 0,\mathop {\max }\limits_{\left[ {0;3} \right]} y = 20\).
Câu 14.(VD)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với mặt phẳng (ABC), SA=AB=a.
a) Tính thể tích khối chóp S.ABC theo a.
b) Gọi M, N lần lượt là trung điểm của SB và BC. Tính thể tích của khối chóp A.SMNC theo a.
Phương pháp
a) Tính diện tích đáy.
Thể tích hình chóp có diện tích đáy B, chiều cao h là \(V = \dfrac{1}{3}B.h\)
b) Áp dụng công thức tỉ lệ: \(\dfrac{{{V_{A.SMNC}}}}{{{V_{S.ABC}}}} = \dfrac{{{S_{SMNC}}}}{{{S_{SBC}}}}\)
Cách giải
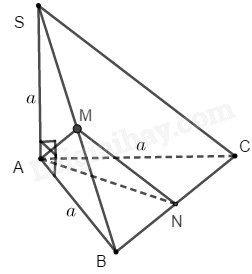
a) Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{{{a^2}}}{2}\)
\({V_{S.ABC}} = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)(đvtt)
b)
\(\begin{array}{l}\dfrac{{MN}}{{SC}} = \dfrac{1}{2} \Rightarrow \dfrac{{{S_{MBN}}}}{{{S_{SBC}}}} = \dfrac{1}{4}\\ \Rightarrow \dfrac{{{S_{SMNC}}}}{{{S_{SBC}}}} = \dfrac{3}{4}\\ \Rightarrow {V_{A.SMNC}} = \dfrac{3}{4}{V_{S.ABC}} = \dfrac{3}{4}.\dfrac{{{a^3}}}{6} = \dfrac{{{a^3}}}{8}\end{array}\)
Câu 15.(VDC)
a) Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ.
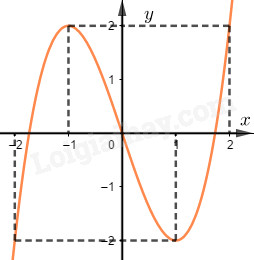
Hỏi phương trình \(\left| {f\left( x \right)} \right| = 2\) có bao nhiêu nghiệm?
b) Cho hàm số \(y = \dfrac{{x - 1}}{{{x^2} - 3{\rm{x}} + m}}\) có đồ thị là \(\left( C \right)\). Tìm tất cả các giá trị của tham số m để tổng số đường tiệm cận đứng và tiệm cận ngang của \(\left( C \right)\) bằng 2.
Phương pháp
a) \(\left| {f\left( x \right)} \right| = a\left( {a > 0} \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\left( {f\left( x \right) \ge 0} \right)\\f\left( x \right) = - a\left( {f\left( x \right) < 0} \right)\end{array} \right.\)
Số nghiệm của phương trình \(f\left( x \right) = a\left( {f\left( x \right) \ge 0} \right)\) bằng số nghiệm của phương trình \(f\left( x \right) = - a\left( {f\left( x \right) < 0} \right)\).
b) Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } y\) để tìm đường tiệm cận ngang.
Tìm điều kiện của m thỏa mãn yêu cầu bài toán.
Cách giải
a) \(\left| {f\left( x \right)} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 2\left( {f\left( x \right) \ge 0} \right)(1)\\f\left( x \right) = - 2\left( {f\left( x \right) < 0} \right)(2)\end{array} \right.\)
Từ đồ thị ta thấy (1) có 2 nghiệm và (2) có 2 nghiệm. Vậy phương trình \(\left| {f\left( x \right)} \right| = 2\) có 4 nghiệm phân biệt.
b) \(\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{x - 1}}{{{x^2} - 3x + m}} = 0\). Đồ thị hàm số có 1 đường tiệm cận ngang.
Khi đó bài toán trở thành: Tìm m để đồ thị hàm số có 1 đường tiệm cận đứng.
\( \Leftrightarrow {x^2} - 3x + m = 0\)(1) có 1 nghiệm bằng 1 và 1 nghiệm khác 1 hoặc phương trình có nghiệm khép khác 1.
TH1: (1) có 1 nghiệm bằng 1 và 1 nghiệm khác 1.
Khi đó, ta có \({1^2} - 3.1 + m = 0 \Leftrightarrow m = 2\). Thử lại ta thấy
\(y = \dfrac{1}{{x - 2}}\) thỏa mãn bài toán.
TH2: (1) có nghiệm kép khác 1.
Khi đó,
\(\left\{ \begin{array}{l}{\Delta _{(1)}} = 0\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 4m = 0\\m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{9}{4}\\m \ne 2\end{array} \right.\).
Vậy \(m = 2\) hoặc \(m = \dfrac{9}{4}\).

