Đề bài
Trong không gian cho hai điểm \(A, B\) cố định và có độ dài \(AB = 20 cm\). Gọi \(d\) là một đường thẳng thay đổi luôn luôn đi qua \(A\) và cách \(B\) một khoảng bằng \(10 cm\). Chứng tỏ rằng đường thẳng \(d\) luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào định nghĩa hình nón: Trong mặt phẳng \((P)\) cho hai đường thẳng \(d\) và \(\Delta\) cắt nhau tại điểm \(O\) vào tạo thành góc \(\beta\) với \({0^0}<{\beta}<{90^0}\).
Khi quay mặt phẳng \((P)\) xung quanh \(\Delta\) thì đường thẳng \(d\) sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh \(O\).
Đường thẳng \(\Delta\) gọi là trục, đường thẳng \(d\) gọi là đường sinh và góc \(2\beta\) gọi là góc ở đỉnh của mặt nón đó.
Lời giải chi tiết
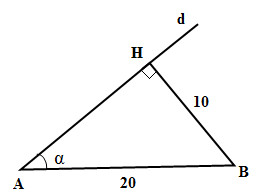
Kẻ \(BH \bot d\) ta có \(BH = 10cm\). Gọi \(\alpha = \widehat {BAH}\)
Ta có \(\sin \alpha = {{BH} \over {AB}} = {1 \over 2} \Rightarrow \alpha = {30^0}=const\).
Đường thẳng \(d\) cắt AB tại điểm A và tạo thành góc \(30^0\) nên đường thẳng \(d\) luôn thuộc mặt nón nhận đường thẳng \(AB\) làm trục và có góc ở đỉnh bằng \(2α = 60^0\)

